
【题目】如图,已知抛物线y=x2+bx+c与坐标轴交于A,B两点,则一元二次方程x2+bx+c=0的根的情况是( )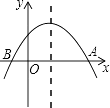
A.没有实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.可能有实数根,也可能没有实数根
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠BAD=90°,对角线BD⊥DC.
(1)求证:△ABD∽△DCB;
(2)如果AD=4,BC=9,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(2)班组织了一次朗读比赛,甲、乙两队各10人的比赛成绩(10分制)如下表(单位:分):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算乙队成绩的平均数和方差;
(3)已知甲队成绩的方差是1.4分2 , 则成绩较为整齐的是队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.

(1)如图1,若∠B=40°,∠C=62°,请说明∠DAE的度数;
(2)如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;
(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,求∠G的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使前两年盈利总额达790万元?若能,求出第二年产品售价;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师为了从平时在班级里数学比较优秀的甲、乙两位同学中选拔一人参加“全国初中数学希望杯竞赛”,对两位同学进行了辅导,并在辅导期间进行了5次测验,两位同学测验成绩得分情况如图所示:
利用表中提供的数据,解答下列问题:
(1)根据右图分别写出甲、乙五次的成绩:
甲: ;乙: .
(2)填写完成下表:
平均成绩 | 中位数 | 众数 | 方差 | |
甲 | 无 | 4 | ||
乙 | 13 |
(3)请你根据上面的信息,运用所学的统计知识,帮助王老师做出选择,并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,与AC交于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:数学活动课上,乐老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.
理解:
(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;
(2)如图2,在圆内接四边形ABCD中,AB是⊙O的直径,AC=BD.求证:四边形ABCD是对等四边形;
(3)如图3,在Rt△PBC中,∠PCB=90°,BC=11,tan∠PBC= ![]() ,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD的长.
,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索发现:如图是一种网红弹弓的实物图,在两头上系上皮筋,拉动皮筋可形成平面示意图如图1图2,弹弓的两边可看成是平行的,即AB∥CD.各活动小组探索∠APC 与∠A,∠C之间的数量关系.已知AB∥CD,点P不在直线AB和直线CD上,在图1中,智慧小组发现:∠APC=∠A+∠C.

智慧小组是这样思考的:过点 P 作 PQ∥AB,……
(1)请你按照智慧小组作的辅助线完成证明过程.
(2)①在图2中,猜测∠APC与∠A,∠C 之间的数量关系,并完成证明.
②如图3,已知AB∥CD,则角α、β、γ之间的数量关系为 .(直接填空)
(3)善思小组提出:如图4,图5.AB∥CD,AF,CF分别平分∠BAP,∠DCP
①在图4中,猜测∠AFC与∠APC之间的数量关系,并证明.
②在图5中,∠AFC与∠APC之间的数量关系为 .(直接填空)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com