练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
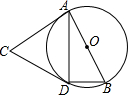
    17．如图，AB是⊙O的直径，点C为⊙O外一点，CA、CD是⊙O的切线，A、D为切点，连接BD、AD．若∠ACD=48°，则∠DBA的大小是（　　）
    A．48°B．60°C．66°D．32°

    分析 构建切线长定理可知CA=CD，求出∠CAD，再证明∠DBA=∠CAD即可解决问题．

    解答 解：∵CA、CD是⊙O的切线，
    ∴CA=CD，
    ∵∠C=48°，
    ∴∠CAD=∠CDA=66°，
    ∵CA⊥AB，AB是直径，
    ∴∠ADB=∠CAB=90°，
    ∴∠DBA+∠DAB=90°，∠CAD+∠DAB=90°，
    ∴∠DBA=∠CAD=66°，
    故选C．

    点评 本题考查切线的性质、等腰三角形的性质、直径所对的圆周角是直角等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    7．将抛物线y=-2x2先向左平移1个单位，再向上平移3个单位，两次平移后得到的抛物线的解析式为（　　）
    A．y=-2（x+1）2+3B．y=-2（x+1）2-3C．y=-2（x-1）2+3D．y=-2（x-1）2-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．下面数据中，是精确数据的是（　　）
    A．2002年美国在阿富汗的战争中每月耗费10亿美元
    B．人的大脑有10000000000个细胞
    C．小明买了5本小说
    D．有关部门预测，2012年以DVD形式出售的影片将首次超过盒式录像带，达到95亿美元

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

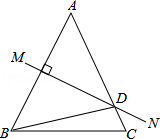    5．如图，等腰△ABC中，AB=AC，AB的垂直平分线MN交AC于点D，∠DBC=15°，则∠A的度数是（　　）
    A．35°B．40°C．50°D．55°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图所示，线段AC的垂直平分线交AB于点D，∠A=43°，则∠BDC的度数为（　　）
    A．90°B．60°C．86°D．43°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知线段AB=6cm，反向延长线段AB到C，使BC=$\frac{8}{3}$AB，D是BC的中点，则线段AD的长为（　　）cm．
    A．2B．3C．5D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．八（3）班第四组10名同学在“爱心捐款”活动中，捐款情况统计如下表，则捐款数组成的数据中，中位数与众数分别是（　　）
    捐款（元）51050100
    人数1432
    A．100，50B．30，10C．10，10D．10，50

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．已知两直角边长分别是整数a，b（b＜2011），则斜边是b+1的直角三角形的个数为31．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．点P为图①中抛物线y=x2-2mx+m2（m为常数，m＞0）上任 一点，将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点（点A在点B的上方），点Q为点P旋转后的对应点．
    （1）若点Q的坐标为（-2，$\sqrt{6}$），求该抛物线的函数关系式；
    （2）如图②，若原抛物线恰好也经过A点，点Q在第一象限内，是否存在这样的点P使得△AGQ是以AG为底的等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案