
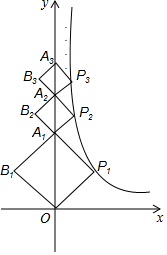
 ��ͼ���ı���OP1A1B1��A1P2A2B2��A2P3A3B3������An-1PnAnBn���������Σ��Խ���OA1��A1A2��A2A3������An-1An����y���ϣ�n��1������������P1��x1��y1������P2��x2��y2��������Pn��xn��yn���ڷ���������y=$\frac{k}{x}$��x��0����ͼ���ϣ�����֪B1��-1��1����
��ͼ���ı���OP1A1B1��A1P2A2B2��A2P3A3B3������An-1PnAnBn���������Σ��Խ���OA1��A1A2��A2A3������An-1An����y���ϣ�n��1������������P1��x1��y1������P2��x2��y2��������Pn��xn��yn���ڷ���������y=$\frac{k}{x}$��x��0����ͼ���ϣ�����֪B1��-1��1�������� ��1�����ı���OP1A1B1Ϊ��������OA1�ǶԽ���֪B1��P1����y��Գƣ��ó���P1��1��1�����ݴ˿ɵô𰸣�
��2������P2B2��P3B3���ֱ�y���ڵ�E��F���ɵ�P1���꼰�����ε�����֪OA1=2���ݴ˿���P2������Ϊ��a��a+2�����������ʽ���a��ֵ���ɣ�ͬ���ɵõ�P3�����ꣻ
��3����${S}_{��{P}_{1}{B}_{1}O}$=2${S}_{��{P}_{1}CO}$=2��$\frac{1}{2}$=1��${S}_{��{P}_{2}{B}_{2}O}$=2${S}_{��{P}_{2}EO}$=2��$\frac{1}{2}$=1��֪��PnBnO�����Ϊ1������P1��1��1����P2��$\sqrt{2}$-1��$\sqrt{2}$+1����P3��$\sqrt{3}$-$\sqrt{2}$��$\sqrt{3}$+$\sqrt{2}$��֪��Pn������Ϊ��$\sqrt{n}$-$\sqrt{n-1}$��$\sqrt{n}$+$\sqrt{n-1}$����
��� �⣺��1����������OP1A1B1�У�OA1�ǶԽ��ߣ�
��B1��P1����y��Գƣ�
��B1��-1��1����
��P1��1��1����
��k=1��1=1������������������ʽΪy=$\frac{1}{x}$��
��2������P2B2��P3B3���ֱ�y���ڵ�E��F��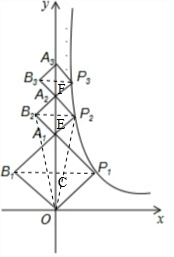
�ֵ�P1������Ϊ��1��1����
��OA1=2��
���P2��������a��a+2����
����y=$\frac{1}{x}$��a=$\sqrt{2}$-1��
�ʵ�P2������Ϊ��$\sqrt{2}$-1��$\sqrt{2}$+1����
��A1E=A2E=2$\sqrt{2}$-2��OA2=OA1+A1A2=2$\sqrt{2}$��
���P3��������b��b+2$\sqrt{2}$����
����y=$\frac{1}{x}$��x��0���ɵ�b=$\sqrt{3}$-$\sqrt{2}$��
�ʵ�P3������Ϊ��$\sqrt{3}$-$\sqrt{2}$��$\sqrt{3}$+$\sqrt{2}$��
��3����${S}_{��{P}_{1}{B}_{1}O}$=2${S}_{��{P}_{1}CO}$=2��$\frac{1}{2}$=1��${S}_{��{P}_{2}{B}_{2}O}$=2${S}_{��{P}_{2}EO}$=2��$\frac{1}{2}$=1����
���PnBnO�����Ϊ1��
��P1��1��1����P2��$\sqrt{2}$-1��$\sqrt{2}$+1����P3��$\sqrt{3}$-$\sqrt{2}$��$\sqrt{3}$+$\sqrt{2}$��֪��Pn������Ϊ��$\sqrt{n}$-$\sqrt{n-1}$��$\sqrt{n}$+$\sqrt{n-1}$����
�ʴ�Ϊ��1����$\sqrt{n}$-$\sqrt{n-1}$��$\sqrt{n}$+$\sqrt{n-1}$����
���� ������Ҫ���鷴��������ϵ��k�ļ������塢����ϵ������������ʽ�������ε����ʣ��������������ε�������������������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
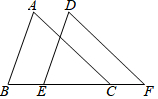 ��ͼ����B��E��C��F��ͬһ��ֱ���ϣ�AB=DE��AC=DF����A=��D��
��ͼ����B��E��C��F��ͬһ��ֱ���ϣ�AB=DE��AC=DF����A=��D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
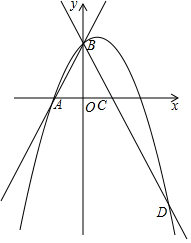 ��ͼ��ֱ��y=2x+2��x�ύ�ڵ�A���� y�ύ�ڵ�B���ѡ�AOB��y�ᷭ������A�䵽C�㣬����B��������y=-x2+bx+c��ֱ��BC���ڵ�D��3��-4����
��ͼ��ֱ��y=2x+2��x�ύ�ڵ�A���� y�ύ�ڵ�B���ѡ�AOB��y�ᷭ������A�䵽C�㣬����B��������y=-x2+bx+c��ֱ��BC���ڵ�D��3��-4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $3\sqrt{15}��\sqrt{3}=3\sqrt{5}$ | B�� | a2��a3=a6 | C�� | a2+a=a3 | D�� | ��-2a2��3=-6a6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
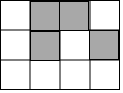 ��ͼ����4��3�����������У���ѡȡһ����ɫ��С�����β�Ϳ�ڣ�ʹͼ�к�ɫ���ֵ�ͼ�ι���һ����Գ�ͼ�εĸ����ǣ�������
��ͼ����4��3�����������У���ѡȡһ����ɫ��С�����β�Ϳ�ڣ�ʹͼ�к�ɫ���ֵ�ͼ�ι���һ����Գ�ͼ�εĸ����ǣ�������| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{12}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com