
【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
【答案】(1)男式单车2000元/辆,女式单车1500元/辆;(2)该社区共有4种购置方案,其中购置男式单车13辆、女式单车9辆时所需总费用最低,最低费用为39500元.
【解析】试题分析:(1)设男式单车x元/辆,女式单车y元/辆,根据“购买3辆男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元”列方程组求解可得;(2)设购置女式单车m辆,则购置男式单车(m+4)辆,根据“两种单车至少需要22辆、购置两种单车的费用不超过50000元”列不等式组求解,得出m的范围,即可确定购置方案;再列出购置总费用关于m的函数解析式,利用一次函数性质结合m的范围可得其最值情况.
试题解析:(1)设男式单车x元/辆,女式单车y元/辆,
根据题意,得:![]() ,
,
解得:![]() ,
,
答:男式单车2000元/辆,女式单车1500元/辆;
(2)设购置女式单车m辆,则购置男式单车(m+4)辆,
根据题意,得:![]() ,
,
解得:9≤m≤12,
∵m为整数,
∴m的值可以是9、10、11、12,即该社区有四种购置方案;
设购置总费用为W,
则W=2000(m+4)+1500m=3500m+8000,
∵W随m的增大而增大,
∴当m=9时,W取得最小值,最小值为39500,
答:该社区共有4种购置方案,其中购置男式单车13辆、女式单车9辆时所需总费用最低,最低费用为39500元.


科目:初中数学 来源: 题型:
【题目】学习了统计知识后,班主任王老师叫班长就本班同学的上学方式进行了一次调查统计,图1和图2是他通过收集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题: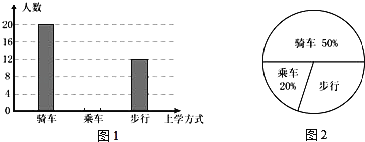
(1)在扇形统计图中,计算出“步行”部分所对应的圆心角的度数;
(2)求该班共有多少名学生;
(3)在图1中,将表示“乘车”的部分补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c,且a>b>c,a+b+c=0,有以下四个命题,则一定正确命题的序号是( )
①x=1是二次方程ax2+bx+c=0的一个实数根;
②二次函数y=ax2+bx+c的开口向下;
③二次函数y=ax2+bx+c的对称轴在y轴的左侧;
④不等式4a+2b+c>0一定成立.
A. ①② B. ①③ C. ①④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c是三角形的三条边,则|a+b﹣c|﹣|c﹣a﹣b|的化简结果为( )
A. 0 B. 2a+2b C. 2c D. 2a+2b﹣2c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三边分别是a,b,c,试化简|a﹣b﹣c|+|b﹣c+a|﹣|c﹣b﹣a|值为( )
A. ﹣a+b+c.B. 3a+b﹣3c.C. ﹣a+b-c.D. ﹣3a﹣b+3c.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过反比例函数y= ![]() (x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2 , 比较它们的大小,可得( )
(x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2 , 比较它们的大小,可得( ) 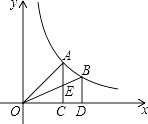
A.S1>S2
B.S1=S2
C.Sl<S2
D.大小关系不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0.
(1)求A、B两点的对应的数a、b;
(2)点C在数轴上对应的数为x,且x是方程2x+1=![]() x﹣8的解.
x﹣8的解.
①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?求出点P对应的数;若不存在,说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com