
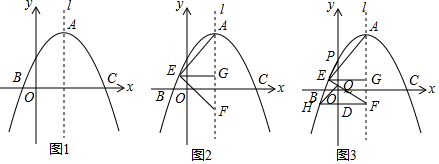
分析 (1)设抛物线解析式为y=a(x-5)2+10(a≠0),然后把点(-1,4)代入抛物线解析式求得a的值即可;
(2)设AG=d,EG=m.结合点A的坐标得到点E的坐标,并将点E的坐标代入函数解析式,经过计算得到d=$\frac{1}{6}$m2.然后由锐角三角函数的定义得到$\frac{EG}{GA}$=$\frac{FG}{EG}$,由此求得FG的长度;
(3)延长HF交抛物线于点N,连接EN,过点E作EM⊥HN,如答图2,构建全等三角形△FQH≌△FME,结合该全等三角形的对应边、角相等、锐角三角函数的定义得到$\frac{HD}{QD}$=$\frac{QD}{DF}$即($\sqrt{{m}^{2}+36}$-5)$\sqrt{{m}^{2}+36}$=36,由此求得$\sqrt{{m}^{2}+36}$=9或$\sqrt{{m}^{2}+36}$=-4(舍去),所以DH=FH-DF=4,当x=-4时,y=-$\frac{1}{6}$(-4-5)2+10=-$\frac{7}{2}$,H(-4,-$\frac{7}{2}$).
解答 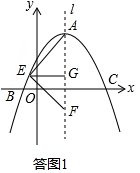 (1)解:设抛物线解析式为y=a(x-5)2+10(a≠0),
(1)解:设抛物线解析式为y=a(x-5)2+10(a≠0),
把点(-1,4)代入,得4=a(-1-5)2+10,
解得a=-$\frac{1}{6}$;
(2)设AG=d,EG=m.如答图1,
∵A的坐标是(5,10),
∴点E的坐标是(5-m,10-d),
∴$\frac{1}{6}$(x-5)2+10=10-d,
解得d=$\frac{1}{6}$m2.
∵AE⊥EF,EG⊥AF,
∴tan∠EAG=tan∠FEG=$\frac{EG}{GA}$=$\frac{FG}{EG}$,
∴EG2=GA•FG,即m2=$\frac{1}{6}$m2FG,
∴FG=6.
(3)延长HF交抛物线于点N,连接EN,过点E作EM⊥HN,如答图2,
由(2)知,AF=$\frac{1}{6}$m+6,且AF=$\frac{1}{6}$HF2,
∴HF=NF=$\sqrt{{m}^{2}+6}$,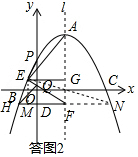
∴HM=$\sqrt{{m}^{2}+36-m}$,MN=$\sqrt{{m}^{2}+36}$+m,
∴MH•MN=$\sqrt{{m}^{2}+36-m}$•($\sqrt{{m}^{2}+36}$+m)=36,
∴MH•MN=36=EM2,
∴$\frac{HM}{EM}$=$\frac{EM}{MN}$,
∴∠ENH=∠HEM,
∴∠HEN=∠HEM+∠MEN=∠ENM+∠MNE=90°,
∴EF=FH=FN,∠HEM=∠ENF=∠HPO=α,
∠EFM=2∠ENF=2α.
∵QH=QP,
∴∠QPH=∠QHP=α,
∴∠HQD=∠QFH=2α,
∴∠HQF=90°,
∴△FQH≌△FME,
∴FQ=FM=m,HQ=EM=FG=6,∠HQF=∠EMF=90°,
∴tan∠HQD=tan∠QFD=$\frac{HD}{QD}$=$\frac{QD}{DF}$,
∴($\sqrt{{m}^{2}+36}$-5)$\sqrt{{m}^{2}+36}$=36,
解得$\sqrt{{m}^{2}+36}$=9或$\sqrt{{m}^{2}+36}$=-4(舍去),
∴FH=9,
∴DH=FH-DF=9-5=4,
当x=-4时,y=-$\frac{1}{6}$(-4-5)2+10=-$\frac{7}{2}$,
∴H(-4,-$\frac{7}{2}$).
点评 本题考查了二次函数综合题,着重考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
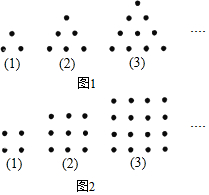 古希腊人常用小石子在沙滩上摆成各种形状来研究数,在图1中,依次摆成第(1),(2),(3),(4)…个三角形状的小石子数3,6,10,…称为三角形数;在图2中,依次摆成第(1),(2),(3),(4),…个正方形状的小石子数4,9,16,…称为正方形数.
古希腊人常用小石子在沙滩上摆成各种形状来研究数,在图1中,依次摆成第(1),(2),(3),(4)…个三角形状的小石子数3,6,10,…称为三角形数;在图2中,依次摆成第(1),(2),(3),(4),…个正方形状的小石子数4,9,16,…称为正方形数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=x2-6x+5的图象与x轴分别相交于A、B两点,且与y轴交于点C.
如图,已知抛物线y=x2-6x+5的图象与x轴分别相交于A、B两点,且与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | $\frac{3}{4}$ | C. | 4 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知线段AB=6cm,延长AB至点C,使BC=AB,反向延长线段AB至D,使AD=AB.
已知线段AB=6cm,延长AB至点C,使BC=AB,反向延长线段AB至D,使AD=AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com