
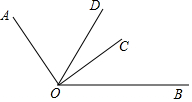
 如图,OD是∠AOB的平分线,∠AOC=2∠BOC,∠COD=22°18′,求∠AOB的度数.
如图,OD是∠AOB的平分线,∠AOC=2∠BOC,∠COD=22°18′,求∠AOB的度数. 分析 设∠BOC=x,然后用x与∠COD的度数分别表示出∠AOD与∠BOD,然后根据角平分线的定义可知∠AOD=∠BOD,计算即可求出x的值,然后求出∠AOC与∠BOC的度数,相加即可得解.
解答 解:设∠BOC=x,则∠AOC=2x,
∵∠COD=22°18′,
∴∠AOD=2x-22°18′,∠BOD=x+22°18′,
∵OD是∠AOB的平分线,
∴∠AOD=∠BOD,
∴2x-22°18′=x+22°18′,
解得x=44°36′,
∴2x=2×44°36=89°12′,
即∠AOC=89°12′,∠BOC=44°36′,
∴∠AOB=∠AOC+∠BOC=133°48′.
点评 本题主要考查了角度的计算,角平分线的定义,分别表示出∠AOD与∠BOD是解题的关键,需要注意度、分、秒是60进制,计算时不要出错.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 画一个三角形其内角和为361° | |
| B. | 任意做一个矩形,其对角线相等 | |
| C. | 任取一个实数,其相反数之和为0 | |
| D. | 外观相同的10件同种产品中有2件是不合格产品,现从中抽取一件恰为合格品 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在平面直角坐标系xOy中,二次函数y=-x2+mx+n的图象经过点A(3,0),B(m,m+1),且与y轴相交于点C.
如图,已知在平面直角坐标系xOy中,二次函数y=-x2+mx+n的图象经过点A(3,0),B(m,m+1),且与y轴相交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
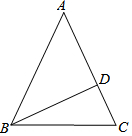 如图,在等腰△ABC中,AB=AC,BD为高.(从下列问题中任选一问作答)
如图,在等腰△ABC中,AB=AC,BD为高.(从下列问题中任选一问作答)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
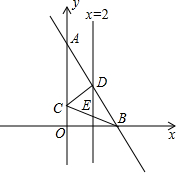 如图,平面直角坐标系中,直线AB:y=-2x+8交y轴于点A,交x轴于点B,以AB为底作等腰三角形△ABC的顶点C恰好落在y轴上,连接BC,直线x=2交AB于点D,交BC于点E,交x轴于点G,连接CD.
如图,平面直角坐标系中,直线AB:y=-2x+8交y轴于点A,交x轴于点B,以AB为底作等腰三角形△ABC的顶点C恰好落在y轴上,连接BC,直线x=2交AB于点D,交BC于点E,交x轴于点G,连接CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com