
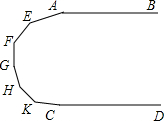
 如图,已知AB∥CD,如果在AB和CD间有五个点E、F、G、H、K,说明:∠A+∠C+∠E+∠F+∠G+∠H+∠K=1080°.
如图,已知AB∥CD,如果在AB和CD间有五个点E、F、G、H、K,说明:∠A+∠C+∠E+∠F+∠G+∠H+∠K=1080°. 分析 过E作EM∥AB,过F作FN∥EM,过G作GO∥FN,过H作HP∥GO,过K作KQ∥GO,根据平行线的性质可得KQ∥CD,可得∠A+∠AEM=180°,∠MEF+∠EFN=180°,∠NFG+∠FGO=180°,∠OGH+∠GHP=180°,∠PHK+∠HKQ=180°,∠QKC+∠C=180°,然后即可求得∠A+∠C+∠E+∠F+∠G+∠H+∠K的度数.
解答 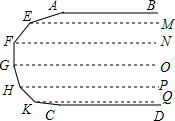 解:E作EM∥AB,过F作FN∥EM,过G作GO∥FN,过H作HP∥GO,过K作KQ∥GO,根据平行线的性质可得KQ∥CD,可得∠A+∠AEM=180°,∠MEF+∠EFN=180°,∠NFG+∠FGO=180°,∠OGH+∠GHP=180°,∠PHK+∠HKQ=180°,∠QKC+∠C=180°,
解:E作EM∥AB,过F作FN∥EM,过G作GO∥FN,过H作HP∥GO,过K作KQ∥GO,根据平行线的性质可得KQ∥CD,可得∠A+∠AEM=180°,∠MEF+∠EFN=180°,∠NFG+∠FGO=180°,∠OGH+∠GHP=180°,∠PHK+∠HKQ=180°,∠QKC+∠C=180°,
∵AB∥CD,
∴KQ∥CD,
∴∠A+∠AEM=180°,∠MEF+∠EFN=180°,∠NFG+∠FGO=180°,∠OGH+∠GHP=180°,∠PHK+∠HKQ=180°,∠QKC+∠C=180°,
∴∠A+∠AEM+∠MEF+∠EFN+∠NFG+∠FGO+∠OGH+∠GHP+∠PHK+∠HKQ+∠QKC+∠C=180°×6=1080°,
即∠A+∠C+∠E+∠F+∠G+∠H+∠K=1080°.
点评 本题考查了平行线的性质,解题的关键是掌握平行线的性质:两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
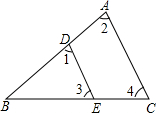 如图,
如图,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
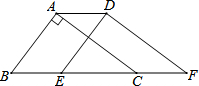 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论①AC∥DF;②ED⊥DF;③四边形ABFD的周长是16.其中正确的个数为( )
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论①AC∥DF;②ED⊥DF;③四边形ABFD的周长是16.其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com