
分析 (1)根据函数的概念和所给的已知条件即可列出关系式,再结合实际即可得出时间t的取值范围;
(2)根据长方形的周长,可得长方形的长,根据长方形的面积公式,可得函数解析式,根据长方形的长小于周长的一半,大于长方形的宽,可得自变量的取值范围.
解答 解:(1)由已知条件知,每小时放50立方米水,
则t小时后放水50t立方米,
而水池中总共有600立方米的水,
那么经过t时后,剩余的水为600-50t,
故剩余水的体积V(m3)与时间t(h)之间的函数关系式为:V=600-50t;
由于t为时间变量,所以t≥0.
又因为当t=12时将水池的水全部抽完了.
故自变量t的取值范围为:0≤t≤12;
(2)长方形的宽为(6-x)cm,
这个长方形的面积y(cm2)与x的函数关系式是y=-x2+6x,
由长方形的长小于长方形的周长的一半,得x<6,
由长方形的长大于长方形的宽,得x>3,
自变量x的取值范围是3<x<6.
故答案为:V=600-50t,0≤t≤12;y=-x2+6x,3<x<6.
点评 本题考查了函数关系式,利用了长方形的面积公式,长方形的长与周长,长方形的长与长方形的宽的关系.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
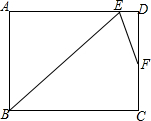 在矩形ABCD中,∠ABC的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F.若AB=9,F是CD的三等分点,则BC=6$\sqrt{2}$+3或3$\sqrt{2}$+6.
在矩形ABCD中,∠ABC的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F.若AB=9,F是CD的三等分点,则BC=6$\sqrt{2}$+3或3$\sqrt{2}$+6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com