
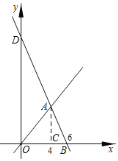
【题目】如图,一次函数的图象交x轴于点B (6,0),交正比例函数的图象于点A,且点A的横坐标为4,S△ABO=12.求一次函数和正比例函数的表达式.
【答案】一次函数的解析式为y=﹣2x+12;正比例函数的解析式为y=x
【解析】
设A(4,yA),利用三角形面积公式得到![]() BO|yA|=12,可解得yA=4,然后利用待定系数法求两个函数解析式.
BO|yA|=12,可解得yA=4,然后利用待定系数法求两个函数解析式.
解:设正比例函数y=kx,一次函数y=ax+b,
∵点A横坐标为4,设A(4,yA),
∵S△AOB=12,
∴![]() BO|yA|=12,即
BO|yA|=12,即![]() ×6×|yA|=12,
×6×|yA|=12,
∴yA=4,
∴A点坐标为(4,4),
把点A(4,4)代入正比例函数y=kx,得4k=4,
解得k=1;
故正比例函数的解析式为y=x;
把点A(4,4)、B(6,0)代入y=ax+b,
得![]() ,
,
解得![]() ,
,
故正比例函数的解析式为y=x,一次函数的解析式为y=﹣2x+12.


科目:初中数学 来源: 题型:
【题目】点D是△ABC中∠BAC的平分线和BC的垂直平分线的交点,DG⊥AB于点G,DH⊥AC交AC的延长线于点H.
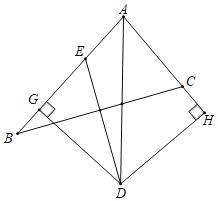
(1)求证:BG=CH;
(2)若AB=12,AC=6,则BG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东海县是“世界水晶之都”,某水晶产业大户经销一种水晶新产品,现准备从国内和国外两种销售方案中选择一种进行销售,若只在国内销售,销售价格y(元/件)与月销售x(件)的函数关系式为y=﹣![]() x+180,成本为30元/件,无论销售多少,每月还需支出广告费6250元,设月利润为w1(元),若只在国外销售,销售价格为180元/件,受各种不确定因素影响,成本为a元/件(a为常数,20≤a≤60),当月销售量为x(件)时,每月还需缴纳
x+180,成本为30元/件,无论销售多少,每月还需支出广告费6250元,设月利润为w1(元),若只在国外销售,销售价格为180元/件,受各种不确定因素影响,成本为a元/件(a为常数,20≤a≤60),当月销售量为x(件)时,每月还需缴纳![]() x2元的附加费,设月利润为w2(元).
x2元的附加费,设月利润为w2(元).
(1)当x=1000时,y= 元/件,w1= 元.
(2)分别求出w1,w2与x间的函数关系式(不必写x的取值范围).
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与国内销售月利润最大值相同,求a的值.(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈2.2).
≈2.2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨(x>14),应交水费为y元,请写出y与x之间的函数关系式;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是□ABCD的边BC延长线上一点,AE交CD于点F,FG∥AD交AB于点G.
(1)填空:图中与△CEF相似的三角形有__________;(写出图中与△CEF相似的所有三角形)
(2)从(1)中选出一个三角形,并证明它与△CEF相似.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,则球的半径长是( )

A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面直角坐标系中有5个点:A(1,1),B(-3,-1),C(-3,1),
D(-2,-2),E(0,-3)。

(1)画出△ABC的外接圆⊙P,并指出点D与⊙P的位置关系;
(2)若直线l经过点D(-2,-2),E(0,-3),判断直线l与⊙P的位置关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为28,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
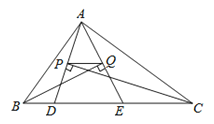
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方位角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com