
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2+![]() x+c����A��0��4����C��8��0����P��t��0����x���������ϵ�һ�����㣬M���߶�AP���е㣬���߶�MP�Ƶ�P˳ʱ����ת90����߶�PB������B��x��Ĵ��ߡ�����A��y��Ĵ��ߣ���ֱ���ཻ�ڵ�D��
x+c����A��0��4����C��8��0����P��t��0����x���������ϵ�һ�����㣬M���߶�AP���е㣬���߶�MP�Ƶ�P˳ʱ����ת90����߶�PB������B��x��Ĵ��ߡ�����A��y��Ĵ��ߣ���ֱ���ཻ�ڵ�D��
��1����������ߵĶԳ��
��2����tΪ��ֵʱ����D�����������ϣ�
��3���Ƿ����t��ʹ����A��B��DΪ��������������PEB���ƣ������ڣ����ʱt��ֵ���������ڣ���˵�����ɣ�

���𰸡���1���Գ���Ϊ��x=![]() ����2����t=3ʱ����D�����������ϣ���3����t=��2+2
����2����t=3ʱ����D�����������ϣ���3����t=��2+2![]() ��t=8+4
��t=8+4![]() ʱ����A��B��DΪ��������������PEB���ƣ�
ʱ����A��B��DΪ��������������PEB���ƣ�
�������������������1�������������ô���ϵ���������������ʽ���Ӷ��õ��Գ����2����������ó���M�����꣬������ת�����ʵó���E�͵�B�����꣬�Ӷ��õ���D�����꣬Ȼ�����t��ֵ����3����0��t��8��t��8���������ÿ���������������������ۼ��㣬�ó�t��ֵ��
�����������1������ã� �����
����� ��
��
![]() �����ߵĽ���ʽΪ��
�����ߵĽ���ʽΪ�� ![]() �����ĶԳ���Ϊ��
�����ĶԳ���Ϊ�� ![]()
��2��������ã� ![]() ��
�� ![]() ��
��
![]() ��
��![]() �Ƶ�P˳ʱ����ת90�����ã�
�Ƶ�P˳ʱ����ת90�����ã� ![]()
![]() ��
�� ![]() ���Ӷ���
���Ӷ���![]() ��
��
����![]() ���������ϣ���
���������ϣ���![]() �� ���
�� ���![]()
��![]() ������
������![]() ʱ����D�����������ϣ�
ʱ����D�����������ϣ�
��3������![]() ʱ����ͼ��
ʱ����ͼ��

![]() ��
��
��1������![]() �ס�ADB����ʱ
�ס�ADB����ʱ![]() ���У�
���� ![]() �� ����
�� ���� ��
��
�����![]() ����ʱ
����ʱ![]() �⡣
�⡣
����![]() �ס�ADB�� ��ʱ
�ס�ADB�� ��ʱ![]() ���У�
���� ![]() �� ����
�� ���� ��
��
����ã� ![]() ������
������![]() ��һԪ���η��̵��б�ʽ
��һԪ���η��̵��б�ʽ![]() ��
��
�������ʽ�ã�![]()
![]() ��
�� ![]() ��
��
����![]() ʱ����ͼ��������POA�ס�ADB
ʱ����ͼ��������POA�ס�ADB![]()
��1������![]() �ס�ADB����ʱ
�ס�ADB����ʱ![]() ���У�
����
![]() ����
���� �������
�������![]() �����
�����![]() ��������ȥ����
��������ȥ����
��2������![]() �ס�ADB��ͬ���ô�ʱ
�ס�ADB��ͬ���ô�ʱ![]() �⡣
�⡣
�ۺ���������![]() ��
��![]() ʱ����A��B��DΪ���������������PEB���ơ�
ʱ����A��B��DΪ���������������PEB���ơ�




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
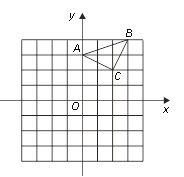
����Ŀ����֪����ABC������ƽ���ڣ��������������ֱ�ΪA��0��3����B��3��4����C��2��2��.�������������У� ÿ��С�����εı߳���1����λ���ȣ�
��1��������ABC����ƽ��4����λ�õ��ġ�A1B1C1����ֱ��д��C1������ꣻ
��2���Ե�BΪλ�����ģ���������������A2BC2��ʹ��A2BC2���ABCλ�ƣ���λ�Ʊ�Ϊ2�U1����ֱ��д��C2������꼰��A2BC2�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC����б��BC=10����BC2+AB2+AC2����(����)
A. 20 B. 100 C. 200 D. 144
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ����_____��
��һ�����ľ���ֵ�������Ǹ�����
������ʽ2x2y�Ĵ�����2��
�������������߶ξͽ�������ľ��룻
��һ����ǵIJ��DZ�������Ǵ�90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A�������ǣ�1��2�������A����x��ĶԳƵ�������ǣ�������
A. ��1����2��B. ����1��2��C. ����1����2��D. ��2��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
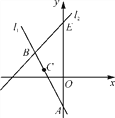
����Ŀ����ͼ��ֱ��l1��ƽ��ֱ������ϵ�У�ֱ��l1��y�ύ�ڵ�A����B(��3��3)Ҳ��ֱ��l1�ϣ�����B������ƽ��1����λ���ȣ�������ƽ��2����λ���ȵõ���C����Cǡ��Ҳ��ֱ��l1�ϣ�
(1)���C�������ֱ��l1�Ľ���ʽ��
(2)��ֱ֪��l2��y��x��b������B����y�ύ�ڵ�E�����ABE�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������̣�m2��9��x2����m��3��x��y=0�ǹ���x,y�Ķ�Ԫһ�η���,��m=_________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���е����±仯������ͬ��Ϊ��ֱ�۱�ʾ��һ������±仯���������Աͨ�������Ƴɣ�������
A.����ͳ��ͼ
B.����ͳ��ͼ
C.����ͳ��ͼ
D.��ʽͳ��ͼ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A�صĺ��θ߶��ǣ�78�ף�B�ر�A�ظ�38�ף�C���ֱ�B�ظ�12�ף���B�صĺ��θ߶���______�ף�C�صĺ��θ߶���______�ף�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com