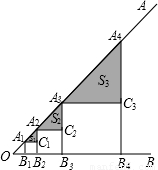
如图,正方形A
1B
1B
2C
1,A
2B
2B
3C
2,A
3B
3B
4C
3,…,A
nB
nB
n+1C
n,按如图所示放置,使点A
1、A
2、A
3、A
4、…、A
n在射线OA上,点B
1、B
2、B
3、B
4、…、B
n在射线OB上.若∠AOB=45°,OB
1=1,图中阴影部分三角形的面积由小到大依次记作S
1,S
2,S
3,…,S
n,则S
n=
.
【答案】
分析:根据正方形性质和等腰直角三角形性质得出OB
1=A
1B
1=1,求出A
1C
1=A
2C
1=1,A
2C
2=A
3C
2=2,A
3C
3=A
4C
3=4,根据三角形的面积公式求出S
1=

×2
×2
,S
2=

×2
1×2
1,S
3=

×2
2×2
2,推出S
n=

×2
n-1×2
n-1,求出即可.
解答:解:∵四边形A
1B
1B
2C
1是正方形,∠O=45°,
∴∠OA
1B
1=45°,
∴OB
1=A
1B
1=1,
同理A
1C
1=A
2C
1=1,
即A
2C
2=1+1=2=A
3C
2,
A
3C
3=A
4C
3=2+2=4,
…,
∴S
1=

×1×1=

×2
×2
,
S
2=

×2×2=

×2
1×2
1S
3=

×4×4=

×2
2×2
2,
S
4=

×8×8=

×2
3×2
3,
…
∴S
n=

×2
n-1×2
n-1=

=2
2n-3.
故答案为:2
2n-3.
点评:本题考查了正方形性质,等腰直角三角形性质,三角形的面积的应用,解此题的关键是能根据求出的结果得出规律,题目比较好,有一定的难度.
练习册系列答案
相关习题
科目:初中数学
来源:
题型:
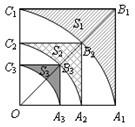
如图,正方形OA
1B
1C
1的边长为2,以O为圆心、OA
1为半径作弧A
1C
1交OB
1于点B
2,设弧A
1C
1与边A
1B
1、B
1C
1围成的阴影部分面积S
1;然后以OB
2为对角线作正方形OA
2B
2C
2,又以O为圆心、OA
2为半径作弧A
2C
2交OB
2于点B
3,设弧A
2C
2与边A
2B
2、B
2C
2围成的阴影部分面积为S
2;…,按此规律继续作下去,设弧A
nC
n与边A
nB
n、B
nC
n围成的阴影部分面积为S
a.则S
1=
,S
2=
,…,S
n=
.
查看答案和解析>>
科目:初中数学
来源:2011-2012学年辽宁省盘锦市四完中九年级(上)第四次月考数学试卷(解析版)
题型:填空题
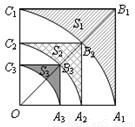
如图,正方形OA
1B
1C
1的边长为2,以O为圆心、OA
1为半径作弧A
1C
1交OB
1于点B
2,设弧A
1C
1与边A
1B
1、B
1C
1围成的阴影部分面积S
1;然后以OB
2为对角线作正方形OA
2B
2C
2,又以O为圆心、OA
2为半径作弧A
2C
2交OB
2于点B
3,设弧A
2C
2与边A
2B
2、B
2C
2围成的阴影部分面积为S
2;…,按此规律继续作下去,设弧A
nC
n与边A
nB
n、B
nC
n围成的阴影部分面积为S
a.则S
1=
,S
2=
,…,S
n=
.
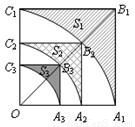
查看答案和解析>>
科目:初中数学
来源:2009-2010学年浙江省丽水市莲都区九年级(上)第三次月考数学试卷(解析版)
题型:填空题
如图,正方形OA
1B
1C
1的边长为2,以O为圆心、OA
1为半径作弧A
1C
1交OB
1于点B
2,设弧A
1C
1与边A
1B
1、B
1C
1围成的阴影部分面积S
1;然后以OB
2为对角线作正方形OA
2B
2C
2,又以O为圆心、OA
2为半径作弧A
2C
2交OB
2于点B
3,设弧A
2C
2与边A
2B
2、B
2C
2围成的阴影部分面积为S
2;…,按此规律继续作下去,设弧A
nC
n与边A
nB
n、B
nC
n围成的阴影部分面积为S
a.则S
1=
,S
2=
,…,S
n=
.
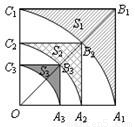
查看答案和解析>>
科目:初中数学
来源:2010年北京市东城区中考数学二模试卷(解析版)
题型:填空题
如图,正方形OA
1B
1C
1的边长为2,以O为圆心、OA
1为半径作弧A
1C
1交OB
1于点B
2,设弧A
1C
1与边A
1B
1、B
1C
1围成的阴影部分面积S
1;然后以OB
2为对角线作正方形OA
2B
2C
2,又以O为圆心、OA
2为半径作弧A
2C
2交OB
2于点B
3,设弧A
2C
2与边A
2B
2、B
2C
2围成的阴影部分面积为S
2;…,按此规律继续作下去,设弧A
nC
n与边A
nB
n、B
nC
n围成的阴影部分面积为S
a.则S
1=
,S
2=
,…,S
n=
.
查看答案和解析>>
科目:初中数学
来源:2010年浙江省杭州市萧山区中考数学模拟试卷47(河庄镇中 陈国亚)(解析版)
题型:填空题
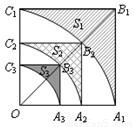
(2010•东城区二模)如图,正方形OA
1B
1C
1的边长为2,以O为圆心、OA
1为半径作弧A
1C
1交OB
1于点B
2,设弧A
1C
1与边A
1B
1、B
1C
1围成的阴影部分面积S
1;然后以OB
2为对角线作正方形OA
2B
2C
2,又以O为圆心、OA
2为半径作弧A
2C
2交OB
2于点B
3,设弧A
2C
2与边A
2B
2、B
2C
2围成的阴影部分面积为S
2;…,按此规律继续作下去,设弧A
nC
n与边A
nB
n、B
nC
n围成的阴影部分面积为S
a.则S
1=
,S
2=
,…,S
n=
.
查看答案和解析>>


 ×2×2,S2=
×2×2,S2= ×21×21,S3=
×21×21,S3= ×22×22,推出Sn=
×22×22,推出Sn= ×2n-1×2n-1,求出即可.
×2n-1×2n-1,求出即可. ×1×1=
×1×1= ×2×2,
×2×2, ×2×2=
×2×2= ×21×21
×21×21 ×4×4=
×4×4= ×22×22,
×22×22, ×8×8=
×8×8= ×23×23,
×23×23, ×2n-1×2n-1=
×2n-1×2n-1= =22n-3.
=22n-3.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案 如图,正方形OA1B1C1的边长为2,以O为圆心、OA1为半径作弧A1C1交OB1于点B2,设弧A1C1与边A1B1、B1C1围成的阴影部分面积S1;然后以OB2为对角线作正方形OA2B2C2,又以O为圆心、OA2为半径作弧A2C2交OB2于点B3,设弧A2C2与边A2B2、B2C2围成的阴影部分面积为S2;…,按此规律继续作下去,设弧AnCn与边AnBn、BnCn围成的阴影部分面积为Sa.则S1=
如图,正方形OA1B1C1的边长为2,以O为圆心、OA1为半径作弧A1C1交OB1于点B2,设弧A1C1与边A1B1、B1C1围成的阴影部分面积S1;然后以OB2为对角线作正方形OA2B2C2,又以O为圆心、OA2为半径作弧A2C2交OB2于点B3,设弧A2C2与边A2B2、B2C2围成的阴影部分面积为S2;…,按此规律继续作下去,设弧AnCn与边AnBn、BnCn围成的阴影部分面积为Sa.则S1=


