
分析 (1)先移项,等式的左边化为完全平方的形式,然后通过直接开平方法解方程;
(2)分解因式后即可得出两个一元一次方程,求出方程的解即可;
(3)先移项,然后通过提取公因式法对等式的左边进行因式分解.
解答 解:(1)由原方程,得
x2-2x=5,
配方,得
x2-2x+1=6,即(x-1)2=6,
开方,得
x-1=±$\sqrt{6}$,
解得x1=1+$\sqrt{6}$,x2=1-$\sqrt{6}$;
(2)由原方程,得
(-2x+1)(-x+1)=0,
-2x+1=0,-x+1=0,
解得x1=$\frac{1}{2}$,x2=1;
(3)3x(x-2)=2(2-x),
(x-2)(3x+2)=0,
解得x1=2,x2=-$\frac{2}{3}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.


科目:初中数学 来源: 题型:选择题
| A. | y1≤y2 | B. | y1=y2 | C. | y1<y2 | D. | y1>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2cm<AB<10cm | B. | 1cm<AB<5cm | C. | 4cm<AB<6cm | D. | 2cm<AB<5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-y)(-x+y) | B. | (-x+y)(x+y) | C. | (x-y)(-x-y) | D. | (x-y)(y+x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3)-2=-9 | B. | m•m-2•m3=m5 | C. | (-a-1b-3)-2=-a2b6 | D. | (-2m)2÷2m3=$\frac{2}{m}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
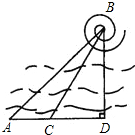 如图,某海滨浴场岸边可近似地看成直线,位于岸边A处的救生员发现海中B处有人求救,1号救生员以6m/秒的速度从A处跑300米到距离B最近的D处,然后游向B处.他在海中游进的速度为2m/秒,∠BAD=45°.
如图,某海滨浴场岸边可近似地看成直线,位于岸边A处的救生员发现海中B处有人求救,1号救生员以6m/秒的速度从A处跑300米到距离B最近的D处,然后游向B处.他在海中游进的速度为2m/秒,∠BAD=45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com