
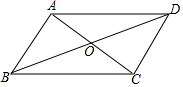
 如图,已知平行四边形ABCD的对角钱AC与BD相交于点O,AB⊥AC,若AB=2,AC=8,则对角线BD的长是( )
如图,已知平行四边形ABCD的对角钱AC与BD相交于点O,AB⊥AC,若AB=2,AC=8,则对角线BD的长是( )| A. | 4$\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
科目:初中数学 来源: 题型:填空题
 按如图所示的程序计算,若开始输入x的值为6,我们发现第一次得到的结果为3,第2次得到的结果为10,第3次得到的结果为5…请你探索第2017次得到的结果为10.
按如图所示的程序计算,若开始输入x的值为6,我们发现第一次得到的结果为3,第2次得到的结果为10,第3次得到的结果为5…请你探索第2017次得到的结果为10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间t(天) | 1 | 5 | 9 | 13 | 17 | 21 |
| 日销售量y(件) | 118 | 110 | 102 | 94 | 86 | 78 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图的正方形网格中,每个小正方形的边长均为1个单位,将△ABC绕点C逆时针旋转90°,得到△A′B′C′;再将△A′B′C′,向右平移2个单位,得到△A″B″C″;请你画出△A′B′C′和△A″B″C″(不要求写画法)
在如图的正方形网格中,每个小正方形的边长均为1个单位,将△ABC绕点C逆时针旋转90°,得到△A′B′C′;再将△A′B′C′,向右平移2个单位,得到△A″B″C″;请你画出△A′B′C′和△A″B″C″(不要求写画法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com