
【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点且AE=BF,连接CE、AF交于点H,连接DH交AG于点O,则下列结论①△ABF≌△CAE;②∠AHC=120°;③AE+CH>CD,中正确的是____.

【答案】①②③
【解析】
由菱形的性质得出CD=AB=BC,由AB=AC,推出AB=BC=AC,即△ABC是等边三角形,同理可得△ADC是等边三角形,则∠B=∠EAC=60°,由SAS即可证得△ABF≌△CAE;得出∠BAF=∠ACE,由外角性质得出∠AEH=∠B+∠BCE,由外角性质得出∠AHC=∠BAF+∠AEH即可得出结果;由△ABF≌△CAE得出AE=BF,由∠AHC=120°得出∠CHF=60°,由△ABC是等边三角形得出∠ACB=60°,则∠HCF<60°,推出∠HFC>60°,则∠HFC>∠CHF得出CH>FC,即可得出结果.
∵四边形ABCD是菱形,
∴CD=AB=BC,
∵AB=AC,
∴AB=BC=AC,
即△ABC是等边三角形,
同理:△ADC是等边三角形,
∴∠B=∠EAC=60°,
在△ABF和△CAE中,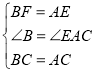 ,
,
∴△ABF≌△CAE(SAS);
故①正确;
∴∠BAF=∠ACE,
∵∠AEH=∠B+∠BCE,
∴∠AHC=∠BAF+∠AEH=∠BAF+∠B+∠BCE=∠B+∠ACE+∠BCE=∠B+∠ACB=60°+60°=120°;
故②正确;
∵△ABF≌△CAE,
∴AE=BF,
∵∠AHC=120°,
∴∠CHF=60°,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠HCF<60°,
∴∠HFC>60°,
∴∠HFC>∠CHF,
∴CH>FC,
∵CD=BC=BF+FC=AE+FC,
∴AE+CH>AE+FC,
即AE+CH>CD;
故③正确;
故答案为①②③.


科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
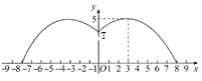
【题目】有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的立杆上点T处汇合.如图所示为截面图,以水平方向为x轴,喷水池中心为原点建立直角坐标系
(1)求水柱所在抛物线(第一象限部分)的函数解析式
(2)正在喷水时,身高1.8米的人,应站在离水池中心多远的地方就能不被淋湿?
(3)在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心的立杆上点T处汇合,请探究扩建后喷水池水柱的最大高度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在寻找下面图中小圆圈个数的规律时,利用了下面图中“分块计数法”,根据小明的方法,猜想并判断下列说法不正确的是( )
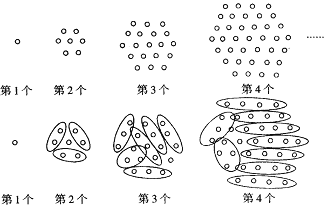
A.第5个图形有61个小圆圈B.第6个图形有91个小圆圈
C.某个图小圆圈的个数可以为271D.某个图小圆圈的个数可以为621
查看答案和解析>>
科目:初中数学 来源: 题型:
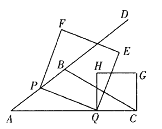
【题目】如图,在![]() 中,
中,![]() =5,
=5,![]() =9,
=9,![]() =
=![]() ,动点
,动点![]() 从
从![]() 出发,沿射线
出发,沿射线![]() 方向以每秒5个单位长度的速度运动,动点
方向以每秒5个单位长度的速度运动,动点![]() 从
从![]() 点出发,一相同的速度在线段
点出发,一相同的速度在线段![]() 上由
上由![]() 向
向![]() 运动,当
运动,当![]() 点运动到
点运动到![]() 点时,
点时,![]() 两点同时停止运动,以
两点同时停止运动,以![]() 为边作正方形
为边作正方形![]() (
(![]() 按逆时针排序),以
按逆时针排序),以![]() 为边在
为边在![]() 上方作正方形
上方作正方形![]() .
.
(1)![]() _______.
_______.
(2)设点![]() 运动时间为
运动时间为![]() ,正方形
,正方形![]() 的面积为
的面积为![]() ,请探究
,请探究![]() 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
(3)当![]() 为何值时,正方形
为何值时,正方形![]() 的某个顶点(
的某个顶点(![]() 点除外)落在正方形
点除外)落在正方形![]() 的边
的边![]() 上,请直接写出
上,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
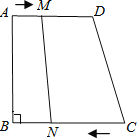
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=15cm,BC=21cm,点M从A点开始,沿AD边向D运动,速度为1厘米/秒,点N从点C开始沿CB边向点B运动,速度为2厘米/秒,设四边形MNCD的面积为S.
(1)写出面积S与时间t之间的函数关系式;
(2)当t为何值时,四边形MNCD是平行四边形?
(3)当t为何值时,四边形MNCD是等腰梯形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线![]() (
(![]() )交x轴于A、B两点,交y轴于点C,且对称轴为直线x=-2 .
)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=-2 .
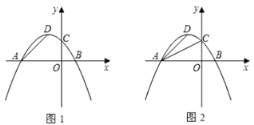
(1)求该抛物线的解析式及顶点D的坐标;
(2)若点P(0,t)是y轴上的一个动点,请进行如下探究:
探究一:如图1,设△PAD的面积为S,令W=t·S,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
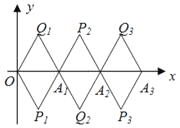
【题目】如图,菱形OP1A1Q1为长为2,且∠P1=60°,将菱形OP1A1Q1绕点A1顺时针旋转1800,得到菱形A1P2A2Q2,将菱形A1P2A2Q2绕点A2顺时针旋转180°,得到菱形A2P3A3Q3……,如此进行下去,直至得到菱形A8P9A9Q9,则:
(1)P1的坐标为_____;
(2)Q9的坐标为_____;
查看答案和解析>>
科目:初中数学 来源: 题型:
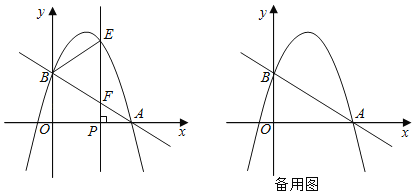
【题目】如图,在平面直角坐标系中,直线![]() 分别交x轴,y轴于点A,B,抛物线y=﹣x2+bx+c经过点A,B,点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
分别交x轴,y轴于点A,B,抛物线y=﹣x2+bx+c经过点A,B,点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
(1)求这条抛物线所对应的函数表达式.
(2)点P在线段OA上时,若以B、E、F为顶点的三角形与△FPA相似,求m的值;
(3)若E、F、P三个点中恰有一点是其它两点所连线段的中点(三点重合除外),称E、F、P三点为“共诸点”.直接写出E、F、P三点成为“共诸点”时m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com