
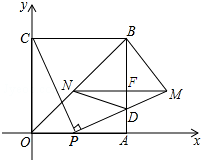
 ИзНјЈ¬ЛДұЯРОOABCКЗұЯіӨОӘ4өДХэ·ҪРОЈ¬өгPОӘOAұЯЙПИОТвТ»өгЈЁУлөгOЎўAІ»ЦШәПЈ©Ј¬Б¬ҪУCPЈ¬№эөгPЧчPMЎНCPҪ»ABУЪөгDЈ¬ЗТPM=CPЈ¬№эөгMЧчMNЎОAOЈ¬Ҫ»BOУЪөгNЈ¬Б¬ҪбNDЎўBMЈ¬ЙиOP=tЈ®
ИзНјЈ¬ЛДұЯРОOABCКЗұЯіӨОӘ4өДХэ·ҪРОЈ¬өгPОӘOAұЯЙПИОТвТ»өгЈЁУлөгOЎўAІ»ЦШәПЈ©Ј¬Б¬ҪУCPЈ¬№эөгPЧчPMЎНCPҪ»ABУЪөгDЈ¬ЗТPM=CPЈ¬№эөгMЧчMNЎОAOЈ¬Ҫ»BOУЪөгNЈ¬Б¬ҪбNDЎўBMЈ¬ЙиOP=tЈ®·ЦОц ЈЁ1Ј©ЧчMEЎНOAУЪөгEЈ¬ТӘЗуөгMөДЧшұкЦ»ТӘЦӨГчЎчOPCЎХЎчEMPјҙҝЙЈ¬ёщҫЭМвДҝЦРөДМхјюҝЙЦӨГчБҪёцИэҪЗРОИ«өИЈ¬ҙУ¶шҝЙТФөГөҪөгMөДЧшұкЈ»
ЈЁ2Ј©КЧПИЕР¶ПКЗ·сұд»ҜЈ¬И»әуХл¶ФЕР¶ПҪбәПМвДҝЦРөДМхјюЛөГчАнУЙјҙҝЙҪвҙрұҫМвЈ»
ЈЁ3Ј©ТӘЗуtОӘәОЦөКұЈ¬ЛДұЯРОBNDMөДГж»эЧоРЎЈ¬Ц»ТӘУГә¬tөДҙъКэКҪұнКҫіцЛДұЯРОөДГж»эЈ¬И»әу»ҜОӘ¶ҘөгКҪјҙҝЙҪвҙрұҫМвЈ»
ЈЁ4Ј©КЧПИРҙіц·ыәПТӘЗуөДөгQөДЧшұкЈ¬И»әуёщҫЭРҙіцөДөгөДЧшұкРҙіцНЖөј№эіМјҙҝЙҪвҙрұҫМвЈ®
Ҫвҙр  ҪвЈәЈЁ1Ј©ИзНј1ЛщКҫЈ¬ЧчMEЎНOAУЪөгEЈ¬
ҪвЈәЈЁ1Ј©ИзНј1ЛщКҫЈ¬ЧчMEЎНOAУЪөгEЈ¬
ЎаЎПMEP=ЎПPOC=90ЎгЈ¬
ЎЯPMЎНCPЈ¬
ЎаЎПCPM=90ЎгЈ¬
ЎаЎПOPC+ЎПMPE=90ЎгЈ¬
УЦЎЯЎПOPC+ЎПPCO=90ЎгЈ¬
ЎаЎПMPE=ЎПPCOЈ¬
ЎЯPM=CPЈ¬
ЎаЎчMPEЎХЎчPCOЈЁAASЈ©Ј¬
ЎаPE=CO=4Ј¬ME=PO=tЈ¬
ЎаOE=4+tЈ¬
ЎаөгMөДЧшұкОӘЈЁ4+tЈ¬tЈ©ЈЁ0ЈјtЈј4Ј©Ј»
ЈЁ2Ј©ПЯ¶ОMNіӨ¶ИІ»ұдЈ¬
АнУЙЈәЎЯOA=AB=4Ј¬
ЎаөгBЈЁ4Ј¬4Ј©Ј¬
ЎаЦұПЯOBөДҪвОцКҪОӘЈәy=xЈ¬
ЎЯөгNФЪЦұПЯOBЙПЈ¬MNЎОOAЈ¬MЈЁ4+tЈ¬tЈ©Ј¬
ЎаөгNЈЁtЈ¬tЈ©Ј¬
ЎЯMNЎОOAЈ¬MЈЁ4+tЈ¬tЈ©Ј¬
ЎаMN=|ЈЁ4+tЈ©-t|=4Ј¬
јҙMNөДіӨ¶ИІ»ұдЈ»
ЈЁ3Ј©УЙЈЁ1Ј©ЦӘЈ¬ЎПMPE=ЎПPCOЈ¬
УЦЎЯЎПDAP=ЎПPOC=90ЎгЈ¬
ЎаЎчDAPЎЧЎчPOCЈ¬
Ўа$\frac{AD}{OP}=\frac{AP}{OC}$Ј¬
ЎЯOP=tЈ¬OC=4Ј¬
ЎаAP=4-tЈ¬
Ўа$\frac{AD}{t}=\frac{4-t}{4}$Ј¬өГAD=$\frac{tЈЁ4-tЈ©}{4}$Ј¬
ЎаBD=4-$\frac{tЈЁ4-tЈ©}{4}$=$\frac{{t}^{2}-4t+16}{4}$Ј¬
ЎЯMNЎОOAЈ¬ABЎНOAЈ¬
ЎаMNЎНBDЈ¬
ЎЯ${S}_{ЛДұЯРОBNDM}=\frac{1}{2}MN•BD$=$\frac{1}{2}ЎБ4ЎБ\frac{{t}^{2}-4t+16}{4}$=$\frac{1}{2}ЈЁt-2Ј©^{2}+6$Ј¬
Ўаөұt=2КұЈ¬ЛДұЯРОBNDMөДГж»эЧоРЎЈ¬ЧоРЎЦө6Ј»
ЈЁ4Ј©ФЪxЦбХэ°лЦбЙПҙжФЪөгQЈ¬К№өГЎчQMNКЗөИСьИэҪЗРОЈ¬ҙЛКұөгQөДЧшұкОӘЈәQ1ЈЁt+2Ј¬0Ј©Ј¬Q2ЈЁ4+t-$\sqrt{16-{t}^{2}}$Ј¬0Ј©Ј¬Q3ЈЁ4+t+$\sqrt{16-{t}^{2}}$Ј¬0Ј©Q4ЈЁt+$\sqrt{16-{t}^{2}}$Ј¬0Ј©ЖдЦРЈЁ0ЈјtЈј4Ј©Ј¬ Q5ЈЁt-$\sqrt{16-{t}^{2}}$Ј¬0Ј©
Q5ЈЁt-$\sqrt{16-{t}^{2}}$Ј¬0Ј©
АнУЙЈәөұЈЁ2Ј©ҝЙЦӘЈ¬OP=tЈЁ0ЈјtЈј4Ј©Ј¬MN=PE=4Ј¬MNЎОxЦбЈ¬ЛщТФ№І·ЦОӘТФПВјёЦЦЗлЈә
өЪТ»ЦЦЗйҝцЈәөұMNОӘөЧұЯКұЈ¬ЧчMNөДҙ№ЦұЖҪ·ЦПЯЈ¬УлxЦбөДҪ»өгОӘQ1Ј¬ИзНј2ЛщКҫ
$P{Q}_{1}=\frac{1}{2}PE=\frac{1}{2}MN$=2Ј¬
ЎаOQ1=t+2Ј¬
ЎаQ1ЈЁt+2Ј¬0Ј©
өЪ¶юЦЦЗйҝцЈәИзНј3ЛщКҫЈ¬өұMNОӘСьКұЈ¬ТФMОӘФІРДЈ¬MNөДіӨОӘ°лҫ¶»ӯ»ЎҪ»xЦбУЪөгQ2ЎўQ3Ј¬Б¬ҪУMQ2ЎўMQ3Ј¬ ФтMQ2=MQ3=4Ј¬
ФтMQ2=MQ3=4Ј¬
ЎаQ2E=$\sqrt{M{{Q}_{2}}^{2}-M{E}^{2}}=\sqrt{16-{t}^{2}}$Ј¬
ЎаOQ2=OE-Q2E=4+t-$\sqrt{16-{t}^{2}}$Ј¬
ЎаQ2ЈЁ4+t-$\sqrt{16-{t}^{2}}$Ј¬0Ј©Ј¬
ЎЯQ3E=Q2EЈ¬
ЎЯOQ3=OE+Q3E=4+t+$\sqrt{16-{t}^{2}}$Ј¬
ЎаQ3ЈЁ4+t+$\sqrt{16-{t}^{2}}$Ј¬0Ј©Ј»
өЪИэЦЦЗйҝцЈ¬өұMNОӘСьКұЈ¬ТФNОӘФІРДЈ¬MNіӨОӘ°лҫ¶»ӯФІ»ЎҪ»xЦбХэ°лЦбУЪөгQ4Ј¬
өұ0ЈјtЈј2$\sqrt{2}$КұЈ¬ИзНј4ЛщКҫЈ¬
ФтPQ4=$\sqrt{N{{Q}_{4}}^{2}-N{P}^{2}}=\sqrt{{4}^{2}-{t}^{2}}$=$\sqrt{16-{t}^{2}}$Ј¬
ЎаOQ4=OP+PQ4=t+$\sqrt{16-{t}^{2}}$Ј¬
јҙQ4ЈЁ$t+\sqrt{16-{t}^{2}}$Ј¬0Ј©Ј®
өұt=2$\sqrt{2}$КұЈ¬
ФтON=4Ј¬ҙЛКұQөгУлOөгЦШәПЈ¬ЙбИҘЈ»
өұ2$\sqrt{2}$ЈјtЈј4КұЈ¬ИзНј5Ј¬ТФNОӘФІРДЈ¬MNОӘ°лҫ¶»ӯ»ЎЈ¬УлxЦбөДҪ»өгОӘQ4Ј¬Q5Ј®
Q4өДЧшұкОӘЈәQ4ЈЁ$t+\sqrt{16-{t}^{2}}$Ј¬0Ј©Ј®
OQ5=t-$\sqrt{16-{t}^{2}}$Ј¬
ЎаQ5ЈЁt-$\sqrt{16-{t}^{2}}$Ј¬0Ј©
ЛщТФЈ¬ЧЫЙПЛщКцЈ¬өұ0ЈјtЈј4КұЈ¬ФЪxЦбөДХэ°лЦбЙПҙжФЪ5ёцөгQЈ¬·ЦұрОӘQ1ЈЁt+2Ј¬0Ј©Ј¬Q2ЈЁ4+t-$\sqrt{16-{t}^{2}}$Ј¬0Ј©Ј¬Q3ЈЁ4+t+$\sqrt{16-{t}^{2}}$Ј¬0Ј©Q4ЈЁt+$\sqrt{16-{t}^{2}}$Ј¬0Ј©Ј¬Q5ЈЁt-$\sqrt{16-{t}^{2}}$Ј¬0Ј©К№ЎчQMNКЗөИСьИэҪЗРОЈ®
өгЖА ұҫМвҝјІйЛДұЯРОЧЫәПМвЈ¬ҪвМвөД№ШјьКЗГчИ·МвТвЈ¬»ӯіцПаУҰөДНјПуЈ¬ХТіцЛщЗуОКМвРиТӘөДМхјюЈ¬АыУГКэРОҪбәПөДЛјПлҪвҙрОКМвЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
 ТСЦӘ·ҙұИАэәҜКэөДБҪЦ§НјПу№ШУЪФӯөг¶ФіЖЈ¬АыУГХвТ»ҪбВЫҪвјҜПВБРОКМвЈәИзНјЈ¬ФЪН¬Т»ЦұҪЗЧшұкПөЦРЈ¬ХэұИАэәҜКэy=kxөДНјПуУл·ҙұИАэәҜКэy=$\frac{\sqrt{3}}{x}$өДНјПу·ЦұрҪ»УЪөЪТ»ЎўИэПуПЮөДөгBЎўDЈ¬ТСЦӘөгAЈЁ-mЈ¬0Ј©ЎўCЈЁmЈ¬0Ј©Ј®
ТСЦӘ·ҙұИАэәҜКэөДБҪЦ§НјПу№ШУЪФӯөг¶ФіЖЈ¬АыУГХвТ»ҪбВЫҪвјҜПВБРОКМвЈәИзНјЈ¬ФЪН¬Т»ЦұҪЗЧшұкПөЦРЈ¬ХэұИАэәҜКэy=kxөДНјПуУл·ҙұИАэәҜКэy=$\frac{\sqrt{3}}{x}$өДНјПу·ЦұрҪ»УЪөЪТ»ЎўИэПуПЮөДөгBЎўDЈ¬ТСЦӘөгAЈЁ-mЈ¬0Ј©ЎўCЈЁmЈ¬0Ј©Ј®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
 ИзНјЈ¬°СТ»ёұИэҪЗ°еИзНјјЧ·ЕЦГЈ¬ЖдЦРЎПACB=DEC=90ЎгЈ¬ЎПA=45ЎгЈ¬ЎПD=30ЎгЈ¬AB=6cmЈ¬DC=7cmЈ®°СИэҪЗ°еDCEИЖөгCЛіКұХлРэЧӘ15ЎгөГөҪЎчDЎдCEЎдЈ¬ИзНјТТЈ¬ХвКұABУлCDЎдПаҪ»УЪөгOЈ¬DЎдEЎдУлABЎўCB·ЦұрПаҪ»УЪөгFЎўGЈ¬Б¬ҪУADЎдЈ®
ИзНјЈ¬°СТ»ёұИэҪЗ°еИзНјјЧ·ЕЦГЈ¬ЖдЦРЎПACB=DEC=90ЎгЈ¬ЎПA=45ЎгЈ¬ЎПD=30ЎгЈ¬AB=6cmЈ¬DC=7cmЈ®°СИэҪЗ°еDCEИЖөгCЛіКұХлРэЧӘ15ЎгөГөҪЎчDЎдCEЎдЈ¬ИзНјТТЈ¬ХвКұABУлCDЎдПаҪ»УЪөгOЈ¬DЎдEЎдУлABЎўCB·ЦұрПаҪ»УЪөгFЎўGЈ¬Б¬ҪУADЎдЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | ЈЁx3Ј©2=x5 | BЈ® | 6x3ЎВЈЁ-3x2Ј©=2x | CЈ® | ЈЁx+yЈ©ЈЁy-xЈ©=y2-x2 | DЈ® | ЈЁ-x-yЈ©2=x2-2xy+y2 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
 ИзНјЈ¬өгDОӘЙдПЯCBЙПТ»өгЈ¬ЗТІ»УлBЎўCЦШәПЈ¬DEЎОABҪ»ЦұПЯCAСУіӨПЯУЪөгE
ИзНјЈ¬өгDОӘЙдПЯCBЙПТ»өгЈ¬ЗТІ»УлBЎўCЦШәПЈ¬DEЎОABҪ»ЦұПЯCAСУіӨПЯУЪөгEІйҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | -3x2+2x-4 | BЈ® | -3x2-2x+4 | CЈ® | -3x2+2x+4 | DЈ® | 3x2-2x+4 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | 5 | BЈ® | 4 | CЈ® | 3 | DЈ® | 2 |
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com