

���� ����������1������CD�����С�CFE=��CDE���ɵó���CFE�Ķ�����
��2������������֤��BEF�ס�AFC�����BE=5+b��AC=b-5���ɵó����ۣ�
�ڷ���ͬ�ٿɵó�BP��AP֮��Ĺ�ϵ��������BP=x�����AB���õ�����x��һԪ���η��̣����۸÷��̵Ľ��������ɣ�
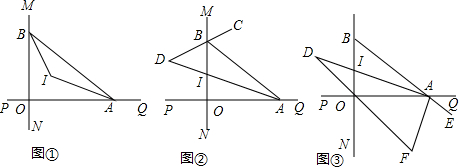
��� �⣺��1������ͼ1������CD�����CFE=��CDE��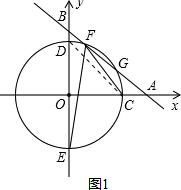
�֡�OD��OC��OC=OD��
���CFE=��CDE=45�㣻
���ɢ�֪��EFC=45�㣬��OB=OA=b��
���OBA=��OAB=45�㣬
���EFC+��CFA=��CFA+��OAF��
���EFA=��FCO��
���EFB=��FCA��
���BEF�ס�AFC��
��$\frac{BE}{BF}=\frac{AF}{AC}$��
�֡�BE=OE+OB=b+5��AC=OA-OC=b-5��
��$\frac{b+5}{BF}=\frac{AF}{b-5}$��
��FA•FB=��b+5����b-5��=b2-25��
��2����ͼ2��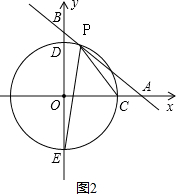
�ɣ�1���ڿɵã�BP•AP=b2-25��
��BP=x����y=-x+b�ɵ�OA=OB=b����Rt��OAB�п����AB=$\sqrt{2}$b����AP=$\sqrt{2}$b-x������BP•AP=b2-25��
�����ɵã�x2-$\sqrt{2}$bx+b2-25=0��
�÷��̵��ж�ʽΪ����=2b2-4��b2-25��=100-2b2��
��b��5$\sqrt{2}$ʱ������0����֪��ʱ������ʵ���⣬����ʱ���߶�AB�ϲ�����ʹ��CPE=45��ĵ�P��
��b=5$\sqrt{2}$ʱ����=0����ʱ����Ϊx2-10x+25=0����ʱ���̵Ľ�Ϊx1=x2=5��
��ʱBP=5��AB=10����AP=5����PΪAB���е㣬
����OP=5���ɹ��ɶ�������õ�P������Ϊ��$\frac{5\sqrt{2}}{2}$��$\frac{5\sqrt{2}}{2}$����
���� ������Ҫ����Բ�ܽǶ��������������ε��ж������ʡ�һ�κ�����֪ʶ���ۺ�Ӧ�ã��ڣ�1�������������Ƶó�FA��FB֮��Ĺ�ϵ�ǽ���Ĺؼ����ڣ�2���аѵ�P�Ĵ������ת��ΪһԪ���η��̵ĸ������⣬������ͼ������Ϊ�����ļ������⣬��������dz��õ������˽������ε����ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{10}$ | B�� | $\sqrt{{a}^{2}+1}$ | C�� | $\sqrt{{x}^{2}+{y}^{2}}$ | D�� | $\sqrt{-2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
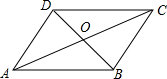 ��ͼ����?ABCD�У�AB=8��BC=6���Խ���AC��BD���ڵ�O������AOD���ܳ�Ϊ16�����AOB���ܳ�Ϊ18��
��ͼ����?ABCD�У�AB=8��BC=6���Խ���AC��BD���ڵ�O������AOD���ܳ�Ϊ16�����AOB���ܳ�Ϊ18���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
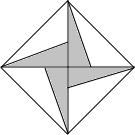 ��֪����ͼ���������е���Ӱ���������ĸ�ֱ�DZ߳�����1��3��ֱ����������ɵģ���ô�������������Ӱ��������ģ�������
��֪����ͼ���������е���Ӱ���������ĸ�ֱ�DZ߳�����1��3��ֱ����������ɵģ���ô�������������Ӱ��������ģ�������| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com