Question

7．如图，已知△ABC，按照下列步骤作图：
①以B为圆心，BA长为半径画弧；
②以C为圆心，CA长为半径画弧，两弧交于点D；
③连接AD，与BC交于点E，连接BD、CD．
（1）求证：△ABC≌△DBC；
（2）若∠ABC=30°，∠ACB=45°，AB=4，求EC的长．

Answer 1

分析 （1）直接运用SSS判定两三角形全等；
（2）根据线段垂直平分线的逆定理得：BC是AD的垂直平分线，得△ABE是直角三角形，△AEC是等腰直角三角形，根据直角三角形中30°角所对的直角边等于斜边的一半求出AE的长，从而得出CE的长．

解答 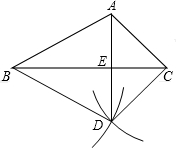证明：（1）由题意得：AB=BD，AC=CD，
∵BC=BC，
∴△ABC≌△DBC；
（2）∵AB=BD，AC=CD，
∴BC是AD的垂直平分线，
∴AD⊥BC，
在Rt△ABE中，∵∠ABE=30°，AB=4，
∴AE=$\frac{1}{2}$AB=2，
∵∠ACB=45°，
∴△AEC是等腰直角三角形，
∴AE=EC，
∵AE=2，
∴EC=2．

点评 本题考查了全等三角形的性质和判定及线段垂直平分线的性质，要熟知全等三角形的判定方法：SSS、SAS、AAS、ASA；在判定两全等三角形全等时，要注意三角形间的公共边和公共角；在直角三角形中，要熟练掌握几下性质：①勾股定理，②等腰直角三角形，③30°角所对的直角边等于斜边的一半．