
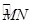 上一动点(B不与点M、N重合),∠MON=90°,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.
上一动点(B不与点M、N重合),∠MON=90°,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.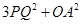 的值.
的值.

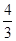

 .
.
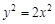 .又
.又 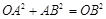 ,
, .
.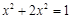 ,
,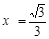 .
.
 ,过点P作OC的平行线分别交BC、GE于点
,过点P作OC的平行线分别交BC、GE于点 、
、 .
.
 .
. ,
,
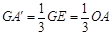 ,
, .
.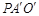 中,
中,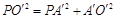 ,
,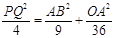 ,
,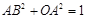 ,
,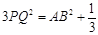 ,
, 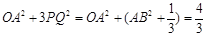 .说明:以上各题的其它解法只要正确.
.说明:以上各题的其它解法只要正确.

 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案科目:初中数学 来源:不详 题型:解答题
 b,得a2-b2=(
b,得a2-b2=( b)2-b2=2b2=b·c.即a2-b2= bc.
b)2-b2=2b2=b·c.即a2-b2= bc.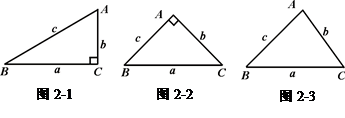
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
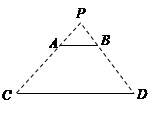
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.有两条边对应成比例的等腰三角形; |
| B.有一个角是25度的等腰三角形; |
| C.有一个角是100度的等腰三角形; |
| D.有一个角相等,两边对应成比例的三角形; |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ABC中,∠C=90°,两直角边AC、BC的长恰是方程
ABC中,∠C=90°,两直角边AC、BC的长恰是方程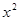 -4x+2=0的两个不同的根,则Rt
-4x+2=0的两个不同的根,则Rt ABC的斜边上的高线CD的长为
ABC的斜边上的高线CD的长为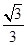 (B)
(B)
 (D)2
(D)2
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com