
 已知:在△ABC中,AB=AC.
已知:在△ABC中,AB=AC. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,A(t,0),B(t+$\sqrt{3}$,0),对于线段AB和x轴上方的点P给出如下定义:当∠APB=60°时,称点P为AB的“等角点”.
在平面直角坐标系xOy中,A(t,0),B(t+$\sqrt{3}$,0),对于线段AB和x轴上方的点P给出如下定义:当∠APB=60°时,称点P为AB的“等角点”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
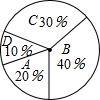 某校260名学生参加植树活动,要求每人植4-7棵,活动结束后随机调查了部分学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.并结合调查数据作出如图所示的扇形统计图,根据统计图提供的信息,可估算出该校植树量达到6棵的学生有( )
某校260名学生参加植树活动,要求每人植4-7棵,活动结束后随机调查了部分学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.并结合调查数据作出如图所示的扇形统计图,根据统计图提供的信息,可估算出该校植树量达到6棵的学生有( )| A. | 26名 | B. | 52名 | C. | 78名 | D. | 104名 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直角梯形ABCD中,∠B=90°,AD∥BC,BC=2AD,点E为边BC的中点.
如图,直角梯形ABCD中,∠B=90°,AD∥BC,BC=2AD,点E为边BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
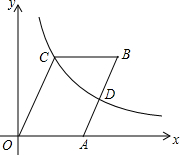 如图,?OABC的顶点B、C在第一象限,点A的坐标为(3,0),D为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点C、D两点,若∠COA=60°,则k的值为4$\sqrt{3}$.
如图,?OABC的顶点B、C在第一象限,点A的坐标为(3,0),D为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点C、D两点,若∠COA=60°,则k的值为4$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com