
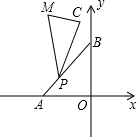
 如图,A(-3,0),B(0,3),C(-1,4),P,C,M按逆时针顺序排列,动点P在线段AB上,∠C=90°,∠CPM=30°,请求出当P点从A运动到B点时,点M运动的路径时什么?并求出M点运动路径长度.
如图,A(-3,0),B(0,3),C(-1,4),P,C,M按逆时针顺序排列,动点P在线段AB上,∠C=90°,∠CPM=30°,请求出当P点从A运动到B点时,点M运动的路径时什么?并求出M点运动路径长度. 分析 如图当点P与A重合时,作MH⊥AB于H,作CM1⊥MH于M1,连接BC,CH,BM1.取AM的中点K,连接KC、KH.当P点从A运动到B点时,点M运动的路径是线段MM1,求出MM1即可解决问题.
解答 解:如图当点P与A重合时,作MH⊥AB于H,作CM1⊥MH于M1,连接BC,CH,BM1.取AM的中点K,连接KC、KH.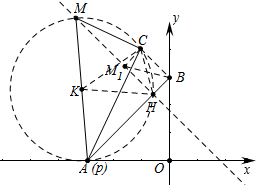
∵KM=KA=KC=KH,
∴A、H、C、M四点共圆,
∴∠CHB=∠AMC=60°,
∵CB=$\sqrt{2}$,
∴BH=BC•tan30°=$\frac{\sqrt{6}}{3}$,AH=AB-BH=3$\sqrt{2}$-$\frac{\sqrt{6}}{3}$,
在Rt△ACB中,AC=$\sqrt{B{C}^{2}+A{B}^{2}}$=2$\sqrt{5}$,
在Rt△ACM中,AM=AC÷cos30°=$\frac{4}{3}$$\sqrt{15}$,
在Rt△AMH中,HM=$\sqrt{A{M}^{2}-A{H}^{2}}$=$\sqrt{6}$+$\sqrt{2}$,
当点P与B重合时,点M与M1重合,易知HM1=BC=$\sqrt{2}$,
∴MM1=HM-HM1=$\sqrt{6}$,
∴当P点从A运动到B点时,点M运动的路径是线段MM1,M点运动路径长度为$\sqrt{6}$.
点评 本题考查轨迹、坐标与图形、圆、锐角三角函数、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加辅助圆解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=$\frac{12±\sqrt{1{2}^{2}-3×4}}{2}$ | B. | x=$\frac{-12±\sqrt{1{2}^{2}-3×4}}{2}$ | ||
| C. | x=$\frac{12±\sqrt{1{2}^{2}+3×4}}{2}$ | D. | x=$\frac{-(-12)±\sqrt{(-12)^{2}-4×3×4}}{2×3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
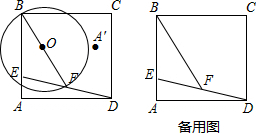
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com