
| A.y1>y2>y3 | B.y1>y3>y2 | C.y3>y2>y1 | D.y3>y1>y2 |
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源:不详 题型:解答题
 销售量】
销售量】| 销售单价x(元/kg) | 10 | 11 | 13 |
| 销售量y(kg) | | | |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
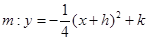 与
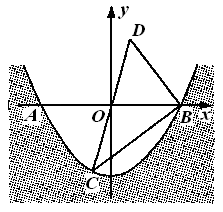
与 轴的交点为A、B,与
轴的交点为A、B,与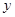 轴的交点为C,顶点为
轴的交点为C,顶点为 ,将抛物线
,将抛物线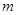 绕点B旋转
绕点B旋转 ,得到新的抛物线
,得到新的抛物线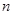 ,它的顶点为D.
,它的顶点为D.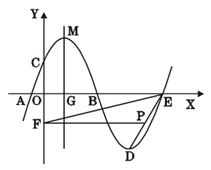
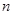 的解析式;
的解析式;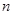 与
与 轴的另一个交点为E,点P是线段ED上一个动点(P不与E、D重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为
轴的另一个交点为E,点P是线段ED上一个动点(P不与E、D重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为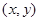 ,△PEF的面积为S,求S与
,△PEF的面积为S,求S与 的函数关系式,写出自变量
的函数关系式,写出自变量 的取值范围;
的取值范围;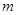 的对称轴与
的对称轴与 轴的交点为G,以G为圆心,A、B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.
轴的交点为G,以G为圆心,A、B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
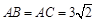 ,经过这个三角形重心的直线DE // BC,分别交边AB、AC于点D和点E,P是线段DE上的一个动点,过点P分别作PM⊥BC,PF⊥AB,PG⊥AC,垂足分别为点M、F、G.设BM = x,四边形AFPG的面积为y.
,经过这个三角形重心的直线DE // BC,分别交边AB、AC于点D和点E,P是线段DE上的一个动点,过点P分别作PM⊥BC,PF⊥AB,PG⊥AC,垂足分别为点M、F、G.设BM = x,四边形AFPG的面积为y.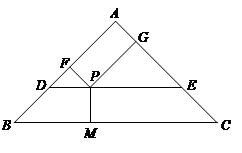
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
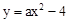 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 x2+1、y2=-
x2+1、y2=- x2-1 与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为 ( )
x2-1 与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为 ( )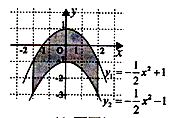
| A.8 | B.6 | C.10 | D.4 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
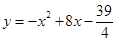 与
与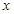 轴所围成的封闭图形染成红色,则在此红色内部区域及其边界上的
轴所围成的封闭图形染成红色,则在此红色内部区域及其边界上的查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

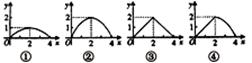
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com