
【题目】如图,直线y=kx+3与x轴,y轴分别交于A,B两点,tan∠OAB= ![]() ,点C(x,y)是直线y=kx+3上与A,B不重合的动点.
,点C(x,y)是直线y=kx+3上与A,B不重合的动点.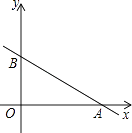
(1)求直线y=kx+3的解析式;
(2)当点C运动到什么位置时△AOC的面积是6;
(3)过点C的另一直线CD与y轴相交于D点,是否存在点C使△BCD与△AOB相似,且△BCD的面积是△AOB的面积的 ![]() ?若存在,请求出点C的坐标;若不存在,请说明理由.
?若存在,请求出点C的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵直线y=kx+3与y轴分别交于B点,
∴B(0,3),
∵tan∠OAB= ![]() ,
,
∴OA=4,
∴A(4,0),
∵直线y=kx+3过A(4,0),
∴4k+3=0,
∴k=﹣ ![]() ,
,
∴直线的解析式为:y=﹣ ![]() x+3
x+3
(2)
解:∵A(4,0),
∴AO=4,
∵△AOC的面积是6,
∴△AOC的高为:3,
∴C点的纵坐标为3,
∵直线的解析式为:y=﹣ ![]() x+3,
x+3,
∴3=﹣ ![]() x+3,
x+3,
x=0,
∴点C运动到B点时,△AOC的面积是6(C是与A、B不重合的动点,所以不符合题意);
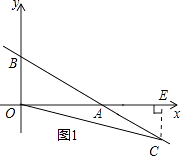
如图1,当C点移动到x轴下方时,作CE⊥x轴于点E,
∵△AOC的面积是6,
∴ ![]() EC×AO=6,
EC×AO=6,
解得:EC=3,
∴C点纵坐标为:﹣3,
∴C点横坐标为:﹣3=﹣ ![]() x+3,
x+3,
∴x=8,
∴点C点坐标为(8,﹣3)时,△AOC的面积是6
(3)
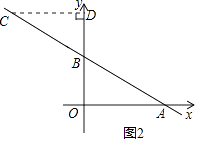
解:①如图2,当CD⊥y轴于点D时,△BCD∽△BAO,
∵△BCD的面积是△AOB的面积的 ![]() ,
,
∴相似比= ![]() ,∴BD=
,∴BD= ![]() BO=1.5,CD=
BO=1.5,CD= ![]() OA=2,
OA=2,
∴C(﹣2,4.5);
②当CD⊥y轴于点D时,△BCD∽△BAO,
∵△BCD的面积是△AOB的面积的 ![]() ,
,
∴相似比= ![]() ,∴BD=
,∴BD= ![]() BO=1.5,CD=
BO=1.5,CD= ![]() OA=2,
OA=2,
∴C点坐标为:(2,1.5);
③当CD⊥AB时,△BDC∽△BAO,
∵△BCD的面积是△AOB的面积的 ![]() ,
,
∴相似比= ![]() ,
,
∴BC=1.5,AC=6.5,
过C作CF⊥OA,
则OB∥CF,
∴CF=3.9,FA=5.2,
∴OF=1.2,
∴C(﹣1.2,3.9);
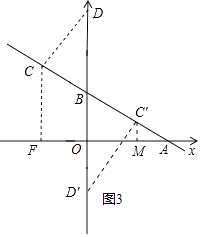
④当DC⊥AB于点C,△BCD∽△BAO,作CM⊥x轴,
当CB=1.5,BD=2.5,
∴BO∥C′M,
则有OM=1.2,C′M=2.1,
∴C(1.2,2.1).
【解析】(1)根据直线y=kx+3与y轴分别交于B点,以及tan∠OAB= ![]() ,即可得出A点坐标,从而得出一次函数的解析式;(2)根据△AOC的面积是6,得出三角形的高,即可求出C点的坐标;(3)利用△BCD与△AOB相似,利用C点不同位置,得出3种不同图形,进而利用相似,得出C点横、纵坐标,进而得出C点坐标.
,即可得出A点坐标,从而得出一次函数的解析式;(2)根据△AOC的面积是6,得出三角形的高,即可求出C点的坐标;(3)利用△BCD与△AOB相似,利用C点不同位置,得出3种不同图形,进而利用相似,得出C点横、纵坐标,进而得出C点坐标.
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小,以及对一次函数的图象和性质的理解,了解一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】一个铝质三角形框架三条边长分别为24cm、30cm、36cm,要估做一个与它相似的铝质三角形框架,现有长为27cm、45cm的两根铝材,要求以其中的一根为一边,从另一根上截下两段(允许有余料)作为另外两边.截法有( )
A.0种
B.1种
C.2种
D.3种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图形中全等的三角形只有两对;②△ABC的面积等于四边形CDOE的面积的两倍;③CD+CE=![]() OA;④AD2+BE2=DE2.其中正确的结论有( )
OA;④AD2+BE2=DE2.其中正确的结论有( )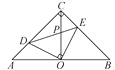
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机张师傅某天上午营运全是在东西向的长江路上进行的,如果向东为正,向西为负,这天上午他行车里程(单位:km)如下:
![]() .
.
⑴.最后一名乘客送到目的地,出租车在东面还是西面?在多少千米处?
⑵.请你帮张师傅算一下,这天上午他一共行驶了多少里程?
⑶.若每千米耗油0.1L,则这天上午张师傅一共用了多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽暑假期间参加社会实践活动,从某批发市场以批发价每个![]() 元的价格购进
元的价格购进![]() 个手机充电宝,然后每个加价
个手机充电宝,然后每个加价![]() 元到市场出售.
元到市场出售.
![]() 求售出
求售出![]() 个手机充电宝的总售价为多少元(结果用含
个手机充电宝的总售价为多少元(结果用含![]() ,
,![]() 的式子表示)?
的式子表示)?
![]() 由于开学临近,小丽在成功售出
由于开学临近,小丽在成功售出![]() 个充电宝后,决定将剩余充电宝按售价
个充电宝后,决定将剩余充电宝按售价![]() 折出售,并很快全部售完.
折出售,并很快全部售完.
①相比不采取降价销售,她将比实际销售多盈利多少元(结果用含![]() 、
、![]() 的式子表示)?
的式子表示)?
②若![]() ,小丽实际销售完这批充电宝的利润率为________(利润率
,小丽实际销售完这批充电宝的利润率为________(利润率![]() 利润
利润![]() 进价
进价![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3.5cm,则此光盘的直径是( )cm. 
A.7
B.![]()
C.![]()
D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
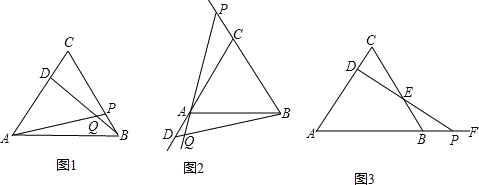
【题目】(9分)探究题:如图:
(1)△ABC为等边三角形,动点D在边CA上,动点P在边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连接AP,BD交于点Q,两点运动过程中AP=BD成立吗?请证明你的结论;
(2)如果把原题中“动点D在边CA上,动点P边BC上,”改为“动点D,P在射线CA和射线BC上运动”,其他条
件不变,如图(2)所示,两点运动过程中∠BQP的大小保持不变.请你利用图(2)的情形,
求证:∠BQP=60°;
(3)如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动,连接PD交BC于E”,其他条件不变,如图(3),则动点D,P在运动过程中,DE始终等于PE吗?写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南安边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向.回答下列问题: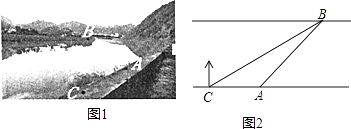
(1)∠CBA的度数为 .
(2)求出这段河的宽(结果精确到1m,备用数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73.
≈1.73.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com