
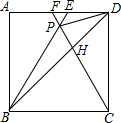
 ��ͼ����������ABCD�У���BPC�ǵȱ������Σ�BP��CP���ӳ��߷ֱ�AD�ڵ�E��F������BD��DP��BD��CF�ཻ�ڵ�H���������н��ۣ�
��ͼ����������ABCD�У���BPC�ǵȱ������Σ�BP��CP���ӳ��߷ֱ�AD�ڵ�E��F������BD��DP��BD��CF�ཻ�ڵ�H���������н��ۣ�| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� �����õȱ������ε������Լ������ε����ʵó���ABE=��DCF=30�㣬��ֱ������ȫ�������ε��ж������ó��𰸣�
�����õȱ������ε����ʽ�������ε����ʵó���DHP=��BHC=75�㣬�����ó��𰸣�
���������������ε��ж������ʽ��������Ǻ�����ϵ�ó��𰸣�
�ܸ���������������㹫ʽ�����ͼ�εõ���BPD�����=��BCP�����+��CDP���-��BCD��������ó��𰸣�
��� �⣺�ߡ�BPC�ǵȱ������Σ�
��BP=PC=BC����PBC=��PCB=��BPC=60�㣬
��������ABCD��
��AB=BC=CD����A=��ADC=��BCD=90��
���ABE=��DCF=30�㣬
�ڡ�ABE���CDF�У�
$\left\{\begin{array}{l}{��A=��ADC}\\{��ABE=��DCF}\\{AB=CD}\end{array}\right.$��
���ABE�ա�DCF���ʢ���ȷ�� ��PC=DC����PCD=30�㣬
��PC=DC����PCD=30�㣬
���CPD=75�㣬
�ߡ�DBC=45�㣬��BCF=60�㣬
���DHP=��BHC=75�㣬
��PD=DH��
���DPH�ǵ��������Σ��ʢ���ȷ��
�ߡ�BPC�ǵȱ������Σ�
��ɵá�FPE=��PFE=60�㣬
���FEP�ǵȱ������Σ�
���FPE�ס�CPB��
��$\frac{PF}{PC}$=$\frac{EF}{BC}$��
��PF=x��PC=y����DC=y��
�ߡ�FCD=30�㣬
��y=$\frac{\sqrt{3}}{2}$��x+y����
�������1-$\frac{\sqrt{3}}{2}$��y=$\frac{\sqrt{3}}{2}$x��
��ã�$\frac{x}{y}$=$\frac{2\sqrt{3}-3}{3}$��
��PF=$\frac{2\sqrt{3}-3}{3}$AB���ʢ���ȷ��
��ͼ����P��PM��CD��PN��BC��
��������ABCD�ı߳���4����BPCΪ�������Σ�
���PBC=��PCB=60�㣬PB=PC=BC=CD=4��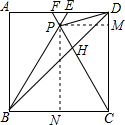
���PCD=30��
��PN=PB•sin60��=4��$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$��PM=PC•sin30��=2��
S��BPD=S�ı���PBCD-S��BCD=S��PBC+S��PDC-S��BCD
=$\frac{1}{2}$��4��2$\sqrt{3}$+$\frac{1}{2}$��2��4-$\frac{1}{2}$��4��4
=4$\sqrt{3}$+4-8=4$\sqrt{3}$-4��
��$\frac{{S}_{��PBD}}{{S}_{�ı���ABCD}}$=$\frac{\sqrt{3}-1}{4}$���ʢ���ȷ��
����ȷ����4����
��ѡ��D��
���� ���⿼���������ε������Լ�ȫ�������ε��ж���֪ʶ��������Ĺؼ������������ߣ�����������Ǻ����Ķ����ʾ����FE��PC�ij��ǽ���ؼ���


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.518��104 | B�� | 5.18��105 | C�� | 51.8��104 | D�� | 518��103 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
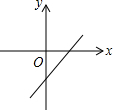 һ�κ���y=kx-��2-b����ͼ����ͼ��ʾ����k��b��ȡֵ��Χ�ǣ�������
һ�κ���y=kx-��2-b����ͼ����ͼ��ʾ����k��b��ȡֵ��Χ�ǣ�������| A�� | k��0��b��2 | B�� | k��0��b��2 | C�� | k��0��b��2 | D�� | k��0��b��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
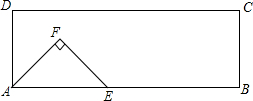 ��ͼ���ھ���ABCD�У�AB=6cm��AD=2cm����E�ӵ�A��ʼ��������AB����ƽ�ƣ���ƽ�ƹ����У����߶�AEΪб������������������AEF����EF����Cʱ����Eֹͣ�ƶ������Eƽ�Ƶľ���Ϊx��cm������AEF�����ABCD�ص����ֵ����Ϊy��cm2����
��ͼ���ھ���ABCD�У�AB=6cm��AD=2cm����E�ӵ�A��ʼ��������AB����ƽ�ƣ���ƽ�ƹ����У����߶�AEΪб������������������AEF����EF����Cʱ����Eֹͣ�ƶ������Eƽ�Ƶľ���Ϊx��cm������AEF�����ABCD�ص����ֵ����Ϊy��cm2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
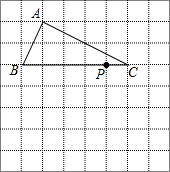 ��ͼ����������ABC����ÿ��С�����εı߳�Ϊ1�������У���A����B����C����P�����ڸ���ϣ�
��ͼ����������ABC����ÿ��С�����εı߳�Ϊ1�������У���A����B����C����P�����ڸ���ϣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com