
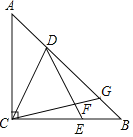
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别在边AB、CB上,CD=DE,∠CDB=∠DEC,过点C作CF⊥DE于点F,交AB于点G,
(1)求证:△ACD≌△BDE;
(2)求证:△CDG为等腰三角形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据题意和图形,利用全等三角形的判定可以证明结论成立;
(2)根据题意和(1)中的结论,利用全等三角形的性质和等腰三角形的判定可以证明结论成立.
证明:(1)∵∠CDB=∠DEC,
∴∠ADC=∠BED,
∵AC=BC,
∴∠A=∠B,
在△ACD与△BDE中,
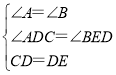 ,
,
∴△ACD≌△BDE(AAS);
(2)由(1)知,△ACD≌△BDE,
∴∠ACD=∠BDE,
∵在Rt△ACB中,AC=BC,
∴∠A=∠B=45°,
∴∠CDG=45°+∠ACD,∠DGC=45°+∠BCG,
∴∠CDF=45°,
∵CF⊥DE交BD于点G,
∴∠DFC=90°,
∴∠DCF=45°,
∵DC=DE,
∴∠DCE=∠DEC,
∵∠DCE=∠DCF+∠BCG=45°+∠BCG,∠DEC=∠B+∠BDE=45°+∠BDE,
∴∠BCG=∠BDE,
∴∠ACD=∠BCG,
∴∠CDG=∠CGD,
∴CD=CG,
∴△CDG是等腰三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC的中点,则下列结论正确的是( )
①△ABD≌△ACD;②∠B=∠C;③∠BAD=∠CAD;④AD⊥BC
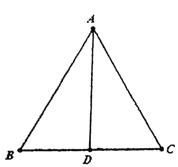
A. ①②③B. ②③④C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在以线段AB为直径的⊙O上取一点,连接AC、BC.将△ABC沿AB翻折后得到△ABD.
(1)试说明点D在⊙O上;
(2)在线段AD的延长线上取一点E,使AB2=AC·AE.求证:BE为⊙O的切线;
(3)在(2)的条件下,分别延长线段AE、CB相交于点F,若BC=2,AC=4,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△PMN中,∠P=90°,PM=PN,MN=6cm,矩形ABCD中AB=2cm,BC=10cm,点C和点M重合,点B、C(M)、N在同一直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线以每秒1cm的速度向右移动,至点C与点N重合为止,设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,则y与x的大致图象是( )
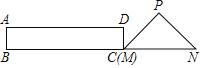
A. 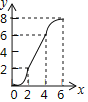 B.
B. 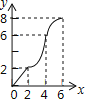 C.
C. 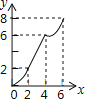 D.
D. 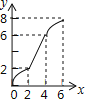
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年5月3日,中国科学院在上海发布了中国首款人工智能芯片:寒武纪(MLU100),该芯片在平衡模式下的等效理论峰值速度达每秒128 000 000 000 000次定点运算,将数
128 000 000 000 000用科学计数法表示为( )
A. 1.28![]() 1014 B. 1.28
1014 B. 1.28![]() 10-14 C. 128
10-14 C. 128![]() 1012 D. 0.128
1012 D. 0.128![]() 1011
1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣1)2过点(3,1),D为抛物线的顶点.
(1)求抛物线的解析式;
(2)若点B、C均在抛物线上,其中点B(0,![]() ),且∠BDC=90°,求点C的坐标;
),且∠BDC=90°,求点C的坐标;
(3)如图,直线y=kx+4﹣k与抛物线交于P、Q两点.
①求证:∠PDQ=90°;
②求△PDQ面积的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点O是原点,顶点B在y轴上,两条对角线AC、OB的长分别是6和4,反比例函数![]() 的图象经过点C.
的图象经过点C.
(1)写出点A的坐标,并求k的值;
(2)将菱形OABC沿y轴向下平移多少个单位长度后点A会落在该反比例函数的图象上?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC先向上平移3个单位长度,再向右平移2个单位长度,得到△A1B1C1.

(1)在图中画出△A1B1C1,并写出点A1、B1、C1的坐标;
(2)连接A1A、C1C,则四边形A1ACC1的面积为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com