
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,点
上,点![]() 、
、![]() 在对角线
在对角线![]() 上,若四边形
上,若四边形![]() 是菱形,则
是菱形,则![]() ________.
________.
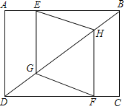
【答案】![]()
【解析】
首先连接EF交BD于O,由矩形ABCD中,四边形EGFH是菱形,易证得△DOF≌△BOE(AAS),即可得OB=OD,然后由勾股定理求得BD的长,继而求得OD的长,又由△DOF∽△DCB,利用相似三角形的对应边成比例,即可求得答案.
连接EF交BD于O, 
∵四边形EGFH是菱形,
∴EF⊥BD,OE=OF,
∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB∥CD,AB=DC=4,
∴∠ABO=∠FDO,
在△OEB与△OFD中,∠EBO=∠FDO,∠EOB=∠FOD,OE=OF,
∴△OEB≌△OFD(AAS),
∴BO=DO,
∵AC2=BC2+DC2=32+42=25,
∴BO=![]() AC=
AC=![]() ,
,
∵∠ODF=∠BDC,∠DOF=∠C=90°,
∴△DOF∽△DCB,
∴![]() =
=![]() ∴BE=DF=
∴BE=DF=![]() ,
,
∴AE=ABBE=4![]() =
=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知点A(3,0),点B(0,3![]() ),点O为原点.动点C、D分别在直线AB、OB上,将△BCD沿着CD折叠,得△B'CD.
),点O为原点.动点C、D分别在直线AB、OB上,将△BCD沿着CD折叠,得△B'CD.

(Ⅰ)如图1,若CD⊥AB,点B'恰好落在点A处,求此时点D的坐标;
(Ⅱ)如图2,若BD=AC,点B'恰好落在y轴上,求此时点C的坐标;
(Ⅲ)若点C的横坐标为2,点B'落在x轴上,求点B'的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E是AD边的中点,BD、CE交于点H,BE、AH交于点G,则下列结论:①AG⊥BE;②BE:BC=![]() :2;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的个数是
:2;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的个数是

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
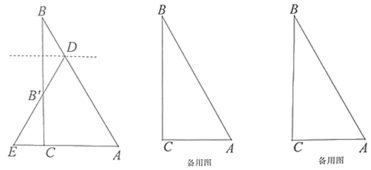
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上,将
上,将![]() 沿着过点
沿着过点![]() 的一条直线翻折,使点
的一条直线翻折,使点![]() 落在射线
落在射线![]() 上的点
上的点![]() 处,连接
处,连接![]() 并延长,交射线
并延长,交射线![]() 于
于![]() .
.
(1)当点![]() 与点
与点![]() 重合时,求BD的长.
重合时,求BD的长.
(2)当点![]() 在
在![]() 的延长线上时,设
的延长线上时,设![]() 为
为![]() ,
,![]() 为
为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出定义域.
的函数关系式,并写出定义域.
(3)连接![]() ,当
,当![]() 是直角三角形时,请直接写出
是直角三角形时,请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
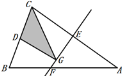
【题目】如图,等腰三角形ABC的底边BC长为4,面积是18,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点G为线段EF上一动点,则△CDG周长的最小值为( )
A.7B.9C.11D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义)配方法是指将一个式子或一个式子的某一部分通过恒等变形化为完全平方式或几个完全平
方式的和,这种方法称之为配方法,例如:可将多项式![]() 通过横档变形化为
通过横档变形化为![]() 的形式,这个变形过程中应用了配方法.
的形式,这个变形过程中应用了配方法.
(1)(理解)对于多项式![]() ,当x=____________时,它的最小值为______________.
,当x=____________时,它的最小值为______________.
(2)(应用)若![]() ,求
,求![]() 的值.
的值.
(3)(拓展)![]() 是
是![]() 的三边,且有
的三边,且有![]() .
.
①若c为整数,求c的值.
②直接写出这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
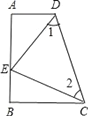
【题目】如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2.
(1)证明:AB=AD+BC;
(2)判断△CDE的形状?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距80km,一辆汽车上午9:00从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了20km/h,并继续匀速行驶至乙地,汽车行驶的路程y(km)与时间x(h)之间的函数关系如图所示,该车到达乙地的时间是当天上午( )
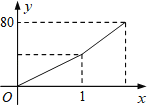
A. 10:35 B. 10:40 C. 10:45 D. 10:50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(m+1)x+m2+2=0.
(1)若方程总有两个实数根,求m的取值范围;
(2)若方程有一个实数根为1,求m的值和另一个根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com