【答案】
分析:(1)用直接开平方法求解就可以了;
(2)先将常数项移到等号的右边,再将二次项系数化为1,然后配方为完全平方公式后直接用开平方法求解就可以;
(3)先化为一般形式,然后确定a、b、c的值,最后带入求根公式求解就可以了;
(4)先移项,然后用平方差公式分解因式就可以求出结论;
(5)设
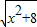
=a,将原方程变形为a
2-a=30,再解一个关于a的一元二次方程求解;
(6)将原方程变形为:(2x
2+1)
2-(2x
2+1)-2=0,再设2x
2+1=a,就可以变为a
2-a-2=0,最后可以运用因式分解法求解.
解答:解:(1)开平方,得
2x-1=±
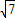
,
∴x
1=
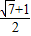
,x
2=
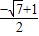
;
(2)移项,得
2x
2-7x=4,
化二次项的系数为1,得
x
2-

x=2,
配方,得
x
2-

x+
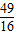
=2+
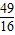
,
(x-

)
2=
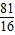
开平方,得
x-

=±

,
∴x
1=4,x
2=-

;
(3)移项,得
2x
2-10x-3=0,
∴a=2,b=-10,c=-3,
∴△=100+24=124>0,
∴x=
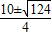
,
∴x
1=
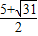
,x
2=
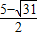
;
(4)移项,得
(3x-4)
2-(3-4x)
2=0
分解因式,得
(3x-4+3-4x)(3x-4-3+4x)=0,
∴-x-1=0或7x-7=0,
∴x
1=-1,x
2=1;
(5)原方程变形为:
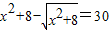
,
设
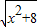
=a,将原方程变形为:
a
2-a=30,
移项,得
a
2-a-30=0,
因式分解,得
(a+5)(a-6)=0,
∴a+5=0或a-6=0,
∴a
1=-5(舍去),a
2=6,
∴
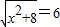
,
解得:x=±2
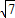
,
经检验,x=±2
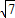
是原方程的根;
(6)原方程变形为:
(2x
2+1)
2-(2x
2+1)-2=0,
设2x
2+1=a,则原方程变为:
a
2-a-2=0,
解得:
a
1=-1,a
2=2,
当a=-1时,
2x
2+1=-1,
△<0,原方程无解,
当a=2时,
2x
2+1=2,
解得:x=±
 点评:
点评:本题考查了换元法、直接开平方法,因式分解法、公式法解一元二次方程和无理方程,在解无理方程时要检验,这是解答者容易忽略的地方.

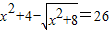 (用换元法解)
(用换元法解) 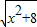 =a,将原方程变形为a2-a=30,再解一个关于a的一元二次方程求解;
=a,将原方程变形为a2-a=30,再解一个关于a的一元二次方程求解;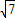 ,
,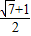 ,x2=
,x2=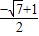 ;
; x=2,
x=2, x+
x+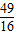 =2+
=2+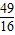 ,
, )2=
)2=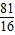
 =±
=± ,
, ;
;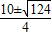 ,
,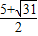 ,x2=
,x2=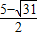 ;
;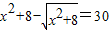 ,
,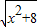 =a,将原方程变形为:
=a,将原方程变形为: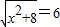 ,
,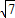 ,
,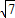 是原方程的根;
是原方程的根;

