
【题目】阅读下面材料:

小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.
请回答:∠O、∠BEO、∠DFO三个角之间的数量关系是 .
参考小亮思考问题的方法,解决问题:
(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;
(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,做∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M= (直接用含α的式子表示).
【答案】(1)∠EOF=∠BEO+∠DFO;(2)65°;(3)90°-![]() α.
α.
【解析】
(1)根据平行线的性质求出∠EOM=∠BEO,∠FOM=∠DFO,即可得出答案;
(2)由DF∥BC,AC∥EF,推出∠EDF=∠B=50°,∠F=∠CGF,推出∠DEF+∠F=180°-50°=130°,再由三角形内角和定理可得∠P+∠FGP=∠F+∠FEP,由此即可解决问题;
(3)由∠M=∠FBM+∠CEM=![]() ∠FBC+
∠FBC+![]() ∠CEM=
∠CEM=![]() (180°-α)=90°-
(180°-α)=90°-![]() α即可解决问题.
α即可解决问题.
(1)如图1中,

∵OP∥AB
∴∠EOP=∠BEO,
∵AB∥CD,
∴OP∥CD,
∴∠FOP=∠DFO,
∴∠EOP+∠FOP=∠BEO+∠DFO,
即:∠EOF=∠BEO+∠DFO;
故答案为:∠EOF=∠BEO+∠DFO.
(2)如图2中,
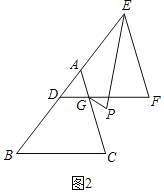
∵DF∥BC,AC∥EF,
∴∠EDF=∠B=50°,∠F=∠CGF,
∴∠DEF+∠F=180°-50°=130°,
∵∠P+∠FGP=∠F+∠FEP,
∴∠P=∠F+∠FEP-∠FGP=![]() ∠DEF+
∠DEF+![]() ∠F=65°.
∠F=65°.
(3)如图3中,
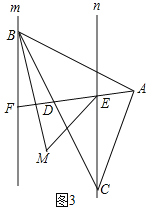
易知∠M=∠FBM+∠CEM,
∵BF∥EC,
∴∠DCE=∠DBF,
∵∠DEC+∠DCE=180°-α,
∠FBM+∠CEM=![]() ∠FBC+
∠FBC+![]() ∠CED=
∠CED=![]() (180°-α)=90°-
(180°-α)=90°-![]() α.
α.
故答案为90°-![]() α.
α.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
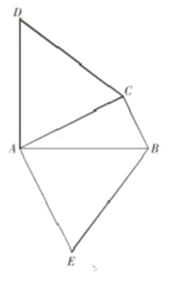
【题目】如图,在△ABC中,DA⊥AB,AD=AB,EA⊥AC,AE=AC.
(1)试说明△ACD≌△AEB;
(2)若∠ACB=90°,连接CE,
①说明EC平分∠ACB;
②判断DC与EB的位置关系,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“2016年联欢会”中,有一个摸奖游戏:有4张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,2张是哭脸,现将4张纸牌洗匀后背面朝上摆放到桌上,然后让同学去翻纸牌.
(1)现在小芳和小霞分别有一次翻牌机会,若正面是笑脸,则小芳获奖;若正面是哭脸,则小霞获奖,她们获奖的机会相同吗?判断并说明理由.
(2)如果小芳、小明都有翻两张牌的机会.翻牌规则:小芳先翻一张,放回后再翻一张;小明同时翻开两张纸牌.他们翻开的两张纸牌中只要出现笑脸就获奖.请问他们获奖的机会相等吗?判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读理解】
我们知道,1+2+3+…+n=![]() ,那么12+22+32+…+n2结果等于多少呢?
,那么12+22+32+…+n2结果等于多少呢?
在图1所示三角形数阵中,第1行圆圈中的数为1,即12,第2行两个圆圈中数的和为2+2,即22,…;第n行n个圆圈中数的和为![]() ,即n2,这样,该三角形数阵中共有
,即n2,这样,该三角形数阵中共有![]() 个圆圈,所有圆圈中数的和为12+22+32+…+n2.
个圆圈,所有圆圈中数的和为12+22+32+…+n2.


【规律探究】
将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n﹣1行的第一个圆圈中的数分别为n﹣1,2,n),发现每个位置上三个圆圈中数的和均为 ,由此可得,这三个三角形数阵所有圆圈中数的总和为:3(12+22+32+…+n2)= ,因此,12+22+32+…+n2= .
【解决问题】
根据以上发现,计算: ![]() 的结果为 .
的结果为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校5月组织了学生参加“学习强国”知识竞赛,从中抽取了部分学生成绩(满分为100分)进行统计,绘制如下不完整的频数直方图,若将频数直方图划分的五组从左至右依次记为A、B、C、D、E,绘制如下扇形统计图,请你根据图形提供的信息,解答下列问题:
(1)频数分布直方图中,A组的频数a= ,并补全频数直方图;
(2)扇形统计图中,D部分所占的圆心角n= 度;
(3)若成绩在80分以上为优秀,全校共有2000名学生,估计成绩优秀的学生有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD,
(1)求抛物线的解析式;
(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,写出自变量x的取值范围,并求当x取多少时,S的值最大,最大是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC=6,BC=9,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区去年购买了A、B两种型号的共享单车,购买A种单车共花费15000元,购买B种单车共花费14000元,购买A种单车的数量是购买B种单车数量的1.5倍,且购买一辆A种单车比购买一辆B种单车少200元.
(1)求去年购买一辆A种和一辆B种单车各需要多少元?
(2)为积极响应政府提出的“绿色发展低碳出行”号召,该社区决定今年再买A、B两种型号的单车共60辆,恰逢厂家对A、B两种型号单车的售价进行调整,A种单车售价比去年购买时提高了10%,B种单车售价比去年购买时降低了10%,如果今年购买A、B两种单车的总费用不超过34000元,那么该社区今年最多购买多少辆B种单车?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com