
 (1)已知a=(-2)3,b=-$\frac{\sqrt{5}}{2}$+$\sqrt{\frac{9}{4}}$,c=${(\sqrt{\frac{17}{2}})}^{2}$,d=|2-$\sqrt{5}$|.
(1)已知a=(-2)3,b=-$\frac{\sqrt{5}}{2}$+$\sqrt{\frac{9}{4}}$,c=${(\sqrt{\frac{17}{2}})}^{2}$,d=|2-$\sqrt{5}$|.分析 (1)直接利用实数运算法则分别化简得出答案;
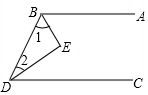
(2)运用角平分线的定义,结合图形可知∠ABD=2∠1,∠BDC=2∠2,又已知∠1+∠2=90°,可得同旁内角∠ABD和∠BDC互补,从而证得AB∥CD.
解答 解:(1)①a=(-2)3=-8,
b=-$\frac{\sqrt{5}}{2}$+$\sqrt{\frac{9}{4}}$=-$\frac{\sqrt{5}}{2}$+$\frac{3}{2}$,
c=${(\sqrt{\frac{17}{2}})}^{2}$=$\frac{17}{2}$,
d=|2-$\sqrt{5}$|=$\sqrt{5}$-2;
②有理数的和m为:-8+$\frac{17}{2}$=$\frac{1}{2}$,
无理数的和n为:-$\frac{\sqrt{5}}{2}$+$\frac{3}{2}$+$\sqrt{5}$-2=$\frac{\sqrt{5}}{2}$-$\frac{1}{2}$,
∵$\sqrt{5}$-1>1,
∴$\frac{\sqrt{5}}{2}$-$\frac{1}{2}$>$\frac{1}{2}$.
(2)AB∥CD,
理由:∵BE平分∠ABD,DE平分∠BDC(已知),
∴∠ABD=2∠1,∠BDC=2∠2(角平分线定义),
∵∠1+∠2=90°,
∴∠ABD+∠BDC=2(∠1+∠2)=180°,
∴AB∥CD(同旁内角互补,两直线平行).
点评 此题主要考查了实数运算,以及平行线的判定,关键是掌握二次根式的化简,掌握同旁内角互补,两直线平行.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
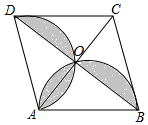 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,分别以AB、AD为直径作一个半圆,则图中阴影部分的面积为( )
如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,分别以AB、AD为直径作一个半圆,则图中阴影部分的面积为( )| A. | $\frac{25}{4}$π-12 | B. | $\frac{16}{3}$π-3 | C. | $\frac{9}{2}$π-6 | D. | $\frac{25}{8}$π-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com