
【题目】如图:抛物线y=- ![]() +bx+c与x轴交于A、B两点,与y轴交于点C,且∠BAC=α,∠ABC=
+bx+c与x轴交于A、B两点,与y轴交于点C,且∠BAC=α,∠ABC= ![]() ,tanα-tanβ=2,∠ACB=90°.
,tanα-tanβ=2,∠ACB=90°.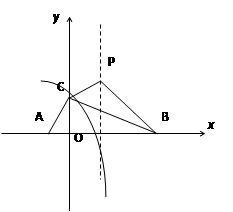
(1)求点C的坐标;
(2)求抛物线的解析式;
(3)若抛物线的顶点为P,求四边形ABPC的面积.
【答案】
(1)解:设A(x1,0), B(x2,0),C(0,b) x1<0,x2>0,b>0
∵ ![]() 、
、 ![]() 是-
是- ![]() +ax+b=0的两根
+ax+b=0的两根
∴ ![]() +
+ ![]() =a,
=a, ![]()
![]() =b
=b
在Rt△ABC中,OC⊥AB
∴OC2=OA·OB
OA=- ![]() ,OB=
,OB= ![]()
∴ ![]() =-
=- ![]()
![]() =b
=b
∵ ![]()
∴b=1
∴C(0,1)
(2)解:Rt△AOC和Rt△BOC中,
tanα-tanβ= ![]() ∴a=2
∴a=2
∴抛物线的解析式为:y=- ![]() +2x+1
+2x+1
(3)解:∵y=- ![]() +2x+1 ∴顶点P的坐标为(1,2)
+2x+1 ∴顶点P的坐标为(1,2)
当- ![]() +2x+1=0时x=1±
+2x+1=0时x=1± ![]() ∴A(1-
∴A(1- ![]() ,0) B(1+
,0) B(1+ ![]() ,0)
,0)
延长PC交x轴于D,直线PC为:y=x+1,点D的坐标为(-1,0)
S四边形ABCD=S△DPB-S△DCA= ![]() DB·yp-
DB·yp- ![]() AD·yc=
AD·yc= ![]() (2+
(2+ ![]() )×2-
)×2- ![]() (2-
(2- ![]() )×1 =
)×1 = ![]()
【解析】(1)设A(x1,0), B(x2,0),C(0,b) x1<0,x2>0,b>0,根据二次函数与一元二次方程的关系知 x 1 、 x 2 是- x 2 +ax+b=0的两根,根据根与系数的关系得 x 1 + x 2 =a, x 1 x 2 =b,判断出△AOC与△COB相似,根据相似三角形对应边成比例得出OC2=OA·OB,从而得出b 2 =- x 1 x 2 =b,又因 b > 0,故b=1,从而得出C点的坐标;
(2)Rt△AOC和Rt△BOC中,tanα-tanβ=![]() =
=![]() =-
=-![]() -
-![]() =
=![]() =2,故a=2,从而得出抛物线的解析式为:y=- x 2 +2x+1;
=2,故a=2,从而得出抛物线的解析式为:y=- x 2 +2x+1;
(3)首先求出抛物线的顶点P的坐标,然后根据坐标轴上点的坐标特点得出A,B的坐标,用待定系数法求出直线PC,进而找到D点的坐标,然后根据S四边形ABCD=S△DPB-S△DCA算出结果
【考点精析】根据题目的已知条件,利用根与系数的关系和确定一次函数的表达式的相关知识可以得到问题的答案,需要掌握一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.如果一条直线与果圆只有一个交点,则这条直线叫做果圆的切线.已知A、B、C、D四点为果圆与坐标轴的交点,E为半圆的圆心,抛物线的解析式为y=x2﹣2x﹣3,AC为半圆的直径.
(1)分别求出A、B、C、D四点的坐标;
(2)求经过点D的果圆的切线DF的解析式;
(3)若经过点B的果圆的切线与x轴交于点M,求△OBM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球每筒的售价多15元,小彬从该网店购买了3筒甲种羽毛球和2筒乙种羽毛球,一共花费270元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定购进甲、乙两种羽毛球各80筒.已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.元旦期间该网店开展优惠促销活动,甲种羽毛球打折销售,乙种羽毛球售价不变,若所购进羽毛球均可全部售出,要使全部售出所购进的羽毛球的利润率是![]() ,那么甲种羽毛球是按原销售价打几折销售的.
,那么甲种羽毛球是按原销售价打几折销售的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4 860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A城气象台测得台风中心在A城正西方向320 km的B处,以每小时40 km的速度向北偏东60°的BF方向移动,距离台风中心200 km的范围内是受台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正比例函数 ![]() 的图象与反比例函数
的图象与反比例函数 ![]()
![]() 在第一象限的图象交于点
在第一象限的图象交于点 ![]() ,过点
,过点 ![]() 作
作 ![]() 轴的垂线,垂足为
轴的垂线,垂足为 ![]() ,已知△OAM的面积为1.
,已知△OAM的面积为1.
(1)求反比例函数的解析式;
(2)如果点 ![]() 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点 ![]() 与点
与点 ![]() 不重合),且点
不重合),且点 ![]() 的横坐标为1,在
的横坐标为1,在 ![]() 轴上求一点
轴上求一点 ![]() ,使
,使 ![]() 最小.
最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣![]() ﹣(+13)+(﹣
﹣(+13)+(﹣![]() )﹣(﹣17)
)﹣(﹣17)
(2)﹣22+3÷(﹣1)2017﹣|﹣4|×5
(3)先化简再求值﹣3(2x2﹣xy)+4(x2+xy﹣6),其中x=﹣1,y=2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com