
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图(1)所示,成本y2与销售月份之间的关系如图(2)所示(图(1)的图象是线段图(2)的图象是抛物线)
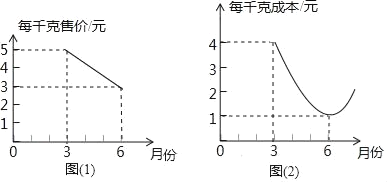
(1)分别求出y1、y2的函数关系式(不写自变量取值范围);
(2)通过计算说明:哪个月出售这种蔬菜,每千克的收益最大?
【答案】(1)y1=![]() ;y2=
;y2=![]() x2﹣4x+13;(2)5月出售每千克收益最大,最大为
x2﹣4x+13;(2)5月出售每千克收益最大,最大为![]() .
.
【解析】
(1)观察图象找出点的坐标,利用待定系数法即可求出y1和y2的解析式;
(2)由收益W=y1-y2列出W与x的函数关系式,利用配方求出二次函数的最大值.
解:(1)设y1=kx+b,将(3,5)和(6,3)代入得,![]() ,解得
,解得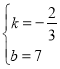 .
.
∴y1=﹣![]() x+7.
x+7.
设y2=a(x﹣6)2+1,把(3,4)代入得,
4=a(3﹣6)2+1,解得a=![]() .
.
∴y2=![]() (x﹣6)2+1,即y2=
(x﹣6)2+1,即y2=![]() x2﹣4x+13.
x2﹣4x+13.
(2)收益W=y1﹣y2,
=﹣![]() x+7﹣(
x+7﹣(![]() x2﹣4x+13)
x2﹣4x+13)
=﹣![]() (x﹣5)2+
(x﹣5)2+![]() ,
,
∵a=﹣![]() <0,
<0,
∴当x=5时,W最大值=![]() .
.
故5月出售每千克收益最大,最大为![]() 元.
元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,顺时针旋转90°,得到△A1B1C1,则旋转中心的坐标是( )
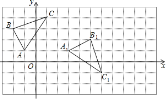
A.(0,0)B.(1,0)C.(1,﹣1)D.(1,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
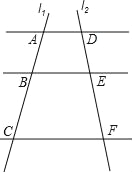
【题目】如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,![]() ,AC=14;
,AC=14;
(1)求AB、BC的长;
(2)如果AD=7,CF=14,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
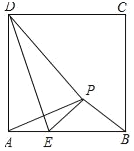
【题目】如图,正方形ABCD中,AD=![]() +2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
+2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() =ax2+bx+c的部分对应值如表,利用二次的数的图象可知,当函数值y>0时,x的取值范围是( )
=ax2+bx+c的部分对应值如表,利用二次的数的图象可知,当函数值y>0时,x的取值范围是( )
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 |
y | ﹣12 | ﹣5 | 0 | 3 | 4 | 3 |
A.0<x<2B.x<0或x>2C.﹣1<x<3D.x<﹣1或x>3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD.
(1)作∠B的平分线交AD于E点。(用尺规作图法,保留作图痕迹,不要求写作法);
(2)若ABCD的周长为10,CD=2,求DE的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
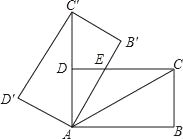
【题目】如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为![]() 的形式:求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解;求解一元二次方程,把它转化为两个一元一次方程来解:求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想一一转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程
的形式:求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解;求解一元二次方程,把它转化为两个一元一次方程来解:求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想一一转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程![]() ,可以通过因式分解把它转化为
,可以通过因式分解把它转化为![]() ,解方程
,解方程![]() 和
和![]() ,可得方程
,可得方程![]() 的解.利用上述材料给你的启示,解下列方程;
的解.利用上述材料给你的启示,解下列方程;
(1)![]() ;
;
(2)![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com