
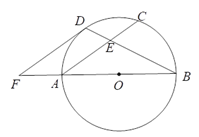
【题目】如图,AB是⊙O的直径,C是⊙O上一点,D是![]() 的中点,BD交AC于点E,过点D作DF∥AC交BA的延长线于点F.
的中点,BD交AC于点E,过点D作DF∥AC交BA的延长线于点F.
(1)求证:DF是⊙O的切线;
(2)若AF=2,FD=4,求tan∠BEC的值.
【答案】(1)证明见解析;(2)tan∠BEC=2
【解析】分析:(1)欲证明DF是⊙O的切线,只要证明OD⊥DF ,OD⊥AC
即可。(2)连接AD,在△ODF中利用勾股定理可求出⊙O的半径,由△ABE∽△FBD可得AE=3,再由△BDA∽△ADE可得![]() ,而∠BEC=∠AED从而即可得出结果。
,而∠BEC=∠AED从而即可得出结果。
本题解析:
(1)证明:连接OD
∵D是![]() 的中点 ∴OD⊥AC
的中点 ∴OD⊥AC
∵DF∥AC ∴OD⊥DF
∵OD为⊙O的半径 ∴直线AB是⊙O的切线
(2)连接AD,设⊙O的半径为r,则OD=OA=r,OF=2+r
∵∠ODF=90°, ∴![]() ,解得:r=3,∴AB=6,BF=8
,解得:r=3,∴AB=6,BF=8
∵DF∥AC,∴△ABE∽△FBD, ∴![]() ,即
,即![]() ,∴AE=3
,∴AE=3
∵D是![]() 的中点,∴∠B=∠DAE ,
的中点,∴∠B=∠DAE ,
∵∠BDA=∠ADE,∴△BDA∽△ADE, ∴![]() ,
,
AB是⊙O的直径, ∴∠ADB=90°, ∴tan∠AED=![]()
∵∠BEC=∠AED,∴tan∠BEC=2


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列图形都是由相同的小正方形按照一定规律摆放而成,其中第1个图共有3个小正方形,第2个图共有8个小正方形,第3个图共有15个小正方形,第4个图共有24个小正方形,…,照此规律排列下去,则第8个图中小正方形的个数是( )
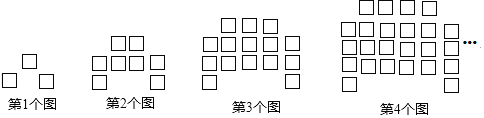
A. 48B. 63C. 80D. 99
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以“迎新年”为主题的艺术活动,举办了四个项目的比赛.它们分别是:A演讲、B唱歌、C书法、D绘画.要求每位同学必须参加且限报一项.以九(一)班为样本进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给出的信息解答下列问题:
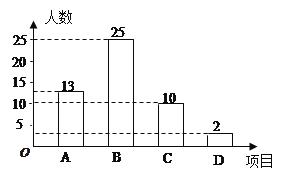
(1)求出参加绘画比赛的学生人数占全班总人数的百分比;
(2)求出扇形统计图中参加书法比赛的学生所在的扇形圆心角的度数;

(3)若该校九年级学生共有500人,请你估计这次活动中参加演讲和唱歌的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于a的方程2(a﹣2)=a+4的解也是关于x的方程2(x﹣3)﹣b=7的解.
(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使![]() =b,点Q为PB的中点,请画出图形并求出线段AQ的长.
=b,点Q为PB的中点,请画出图形并求出线段AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对
,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对![]() ,
,![]() ,都是“共生有理数对”.
,都是“共生有理数对”.
(1)数对![]() ,
,![]() 中是“共生有理数对”的是 ;
中是“共生有理数对”的是 ;
(2)若(m,n)是“共生有理数对”,则(﹣n,﹣m) “共生有理数对”(填“是”或“不是”);
(3)请再写出一对符合条件的“共生有理数对”为 ;(注意:不能与题目中已有的“共生有理数对”重复)
(4)若(a,3)是“共生有理数对”,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年6月28日,深湛高铁正式运营.从湛江到广州全程约468km,高铁开通后,运行时间比特快列车所用的时间减少了6h.若高铁列车的平均速度是特快列车平均速度的3倍,求特快列车与高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
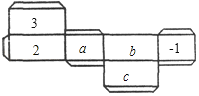
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.
查看答案和解析>>
科目:初中数学 来源: 题型:
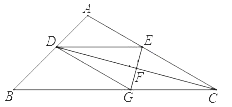
【题目】如图,△ABC中,CD平分∠ACB,CD的垂直平分线分别交AC、DC、BC
于点E、F、G,连接DE、DG.
(1)求证:四边形DGCE是菱形;
(2)若∠ACB=30°,∠B=45°,CG=10,求BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com