
 如图,平行四边形ABCD的顶点A,B的坐标分别是A(-2,0),B(0,-4),顶点C,D在双曲线y=$\frac{k}{x}$上,边AD交y轴于E点,且四边形BCDE的面积是△ABE面积的5倍,则k=48.
如图,平行四边形ABCD的顶点A,B的坐标分别是A(-2,0),B(0,-4),顶点C,D在双曲线y=$\frac{k}{x}$上,边AD交y轴于E点,且四边形BCDE的面积是△ABE面积的5倍,则k=48. 分析 分别过C、D作x轴的垂线,垂足为F、G,过C点作CH⊥DG,垂足为H,根据CD∥AB,CD=AB可证△CDH≌△ABO,则CH=AO=2,DH=OB=4,由此设C(m+2,n),D(m,n+4),C、D两点在双曲线y=$\frac{k}{x}$上,则(m+2)n=m(n+4),解得n=2m,设直线AD解析式为y=ax+b,将A、D两点坐标代入求解析式,确定E点坐标,求S△ABE,根据S四边形BCDE=5S△ABE,列方程求m、n的值,根据k=(m+2)n求解.
解答 解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
∵ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
∴△CDH≌△ABO(AAS),
∴CH=AO=2,DH=OB=4,设C(m+2,n),D(m,n+4),
则(m+2)n=m(n+4)=k,
解得n=2m,则D的坐标是(m,2m+4),
设直线AD解析式为y=ax+b,将A、D两点坐标代入得
$\left\{\begin{array}{l}{-2a+b=0①}\\{ma+b=2m+4②}\end{array}\right.$,
由①得:2a=b,代入②得:ma+2a=2m+4,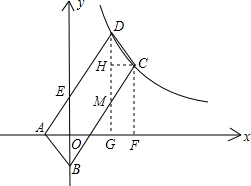
即a(m+2)=2(m+2),解得a=2,
则$\left\{\begin{array}{l}{a=2}\\{b=4}\end{array}\right.$,
∴y=2x+4,E(0,4),BE=8,
∴S△ABE=$\frac{1}{2}$×BE×AO=8,
∵S四边形BCDE=5S△ABE=5×8=40,
∵S四边形BCDE=S△ABE+S四边形BEDM=40,
即8+8×m=40,
解得m=4,
∴n=2m=8,
∴k=(m+2)n=6×8=48.
故答案为:48.
点评 本题考查了反比例函数的综合运用.关键是通过作辅助线,将图形分割,寻找全等三角形,利用边的关系设双曲线上点的坐标,根据面积关系,列方程求解.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:解答题
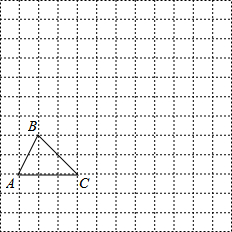 如图,在边长为1个长度单位的小正方形组成的网格中,给出了△ABC(顶点是网格线的交点).
如图,在边长为1个长度单位的小正方形组成的网格中,给出了△ABC(顶点是网格线的交点).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(-a)4÷a2=-a2 | B. | (2a+3b)(2a-3b)=2a2-3b2 | ||
| C. | (xy)-1($\frac{1}{2}$xy)2=$\frac{1}{4}$xy2 | D. | 3ab-2ab=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 数学中,把长与宽之比为$\frac{{\sqrt{5}+1}}{2}$(或宽与长之比为$\frac{{\sqrt{5}-1}}{2}$)的矩形称为黄金矩形.思考解决下列问题:
数学中,把长与宽之比为$\frac{{\sqrt{5}+1}}{2}$(或宽与长之比为$\frac{{\sqrt{5}-1}}{2}$)的矩形称为黄金矩形.思考解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=30°,∠DAE=20°,
如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=30°,∠DAE=20°,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
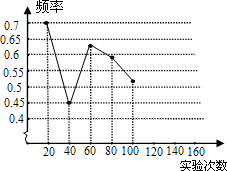 一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:
一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:| 实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
| “車”字朝上的频数 | 14 | 18 | 38 | 47 | 52 | 66 | 78 | 88 |
| 相应的频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | 0.55 | 0.56 | 0.55 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com