
| AP |
| PC |
| AD |
| AO |
| 1 |
| 4 |
| 3 |
| 5 |
| 5 |
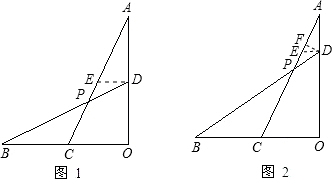 解:(1)过D作DE∥CO交AC于E,
解:(1)过D作DE∥CO交AC于E,| 1 |
| 2 |
| DE |
| CO |
| 1 |
| 2 |
| DE |
| BC |
| 1 |
| 2 |
| PE |
| PC |
| DE |
| BC |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| AP |
| PC |
| AC-PC |
| PC |
| ||
|
| AD |
| AO |
| 1 |
| 4 |
| DE |
| CO |
| AE |
| AC |
| 1 |
| 4 |
| DE |
| BC |
| 1 |
| 4 |
| PE |
| PC |
| DE |
| BC |
| 1 |
| 4 |
| 4 |
| 5 |
| 3 |
| 5 |
| AO2+CO2 |
| (4a)2+(2a)2 |
| 5 |
| AF |
| AO |
| DF |
| CO |
| AD |
| AC |
| a | ||
2
|
2
| ||
| 5 |
| ||
| 5 |
| 5 |
2
| ||
| 5 |
| 3 |
| 5 |
| 5 |
2
| ||
| 5 |
| DF |
| PF |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| AP |
| PC |
| AD |
| AO |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源:2012届贵州省遵义市中考模拟数学卷(带解析) 题型:解答题
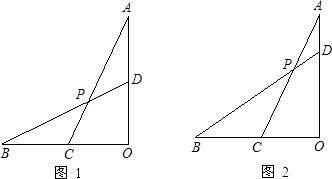
已知线段OA⊥OB,C为OB上中点,D为AO上一点,连AC、BD交于P点.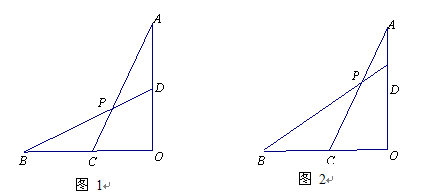
(1)如图1,当OA=OB且D为AO中点时,求 的值;
的值;
(2)如图2,当OA=OB,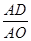 =
= 时,求△BPC与△ACO的面积之比.
时,求△BPC与△ACO的面积之比.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年贵州省遵义市中考模拟数学卷(解析版) 题型:解答题
已知线段OA⊥OB,C为OB上中点,D为AO上一点,连AC、BD交于P点.
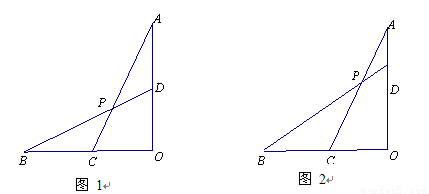
(1)如图1,当OA=OB且D为AO中点时,求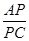 的值;
的值;
(2)如图2,当OA=OB,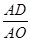 =
=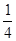 时,求△BPC与△ACO的面积之比.
时,求△BPC与△ACO的面积之比.
查看答案和解析>>
科目:初中数学 来源:2011年3月河南省三门峡市实验中学中考数学模拟试卷(解析版) 题型:解答题
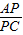 的值;
的值;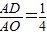 时,求tan∠BPC.
时,求tan∠BPC.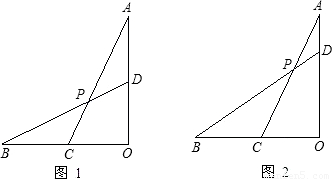
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com