
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:
①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为 ![]() .
.
其中正确的结论有( )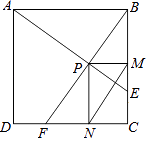
A.2个
B.3个
C.4个
D.5个
【答案】D
【解析】解:如图,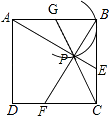
∵动点F,E的速度相同,
∴DF=CE,
又∵CD=BC,
∴CF=BE,
在△ABE和△BCF中,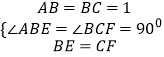
∴△ABE≌△BCF(SAS),故①正确;
∴∠BAE=∠CBF,AE=BF,故②正确;
∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠APB=90°,故③正确;
在△BPE和△BCF中,
∵∠BPE=∠BCF,∠PBE=∠CBF,
∴△BPE∽△BCF,
∴ ![]() =
= ![]() ,
,
∴CFBE=PEBF,
∵CF=BE,
∴CF2=PEBF,故④正确;
∵点P在运动中保持∠APB=90°,
∴点P的路径是一段以AB为直径的弧,
设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,
在Rt△BCG中,CG= ![]() =
= ![]() =
= ![]() ,
,
∵PG= ![]() AB=
AB= ![]() ,
,
∴CP=CG﹣PG= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
即线段CP的最小值为 ![]() ,故⑤正确;
,故⑤正确;
综上可知正确的有5个,
故选D.
由正方形的性质及条件可判断出①△ABE≌△BCF,即可判断出②AE=BF,∠BAE=∠CBF,再根据∠BAE+∠BEA=90°,可得∠CBF+∠BEA=90°,可得出∠APB=90°,即可判断③,由△BPE∽△BCF,利用相似三角形的性质,结合CF=BE可判断④;然后根据点P在运动中保持∠APB=90°,可得点P的路径是一段以AB为直径的弧,设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,最后在Rt△BCG中,根据勾股定理,求出CG的长度,再求出PG的长度,即可求出线段CP的最小值,可判断⑤.


科目:初中数学 来源: 题型:
【题目】某校九年级(1)班准备购买大课间活动器材呼啦圈和跳绳,已知购买1根跳绳和2个呼啦圈要35元,购买2根跳绳和1个呼啦圈要25元.
(1)求每根跳绳、每个呼啦圈各多少元?
(2)根据班级实际情况,需购买跳绳和呼啦圈的总数量为30,总费用不超过300元,但不低于280元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100( ![]() +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
(1)分别求出A与C,A与D间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距离观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触礁的危险?(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两枚正四面体骰子的各面上分别标有数字1,2,3,4,现在同时投掷这两枚骰子,并分别记录着地的面所得的点数为a、b.
(1)假设两枚正四面体都是质地均匀,各面着地的可能性相同,请你在下面表格内列举出所有情形(例如(1,2),表示a=1,b=2),并求出两次着地的面点数相同的概率.
b | 1 | 2 | 3 | 4 |
1 | (1,2) | |||
2 | ||||
3 | ||||
4 |
(2)为了验证试验用的正四面体质地是否均匀,小明和他的同学取一枚正四面体进行投掷试验.试验中标号为1的面着地的数据如下:
试验总次数 | 50 | 100 | 150 | 200 | 250 | 500 |
“标号1”的面着地的次数 | 15 | 26 | 34 | 48 | 63 | 125 |
“标号1”的面着地的频率 | 0.3 | 0.26 | 0.23 | 0.24 |
请完成表格(数字精确到0.01),并根据表格中的数据估计“标号1的面着地”的概率是
查看答案和解析>>
科目:初中数学 来源: 题型:
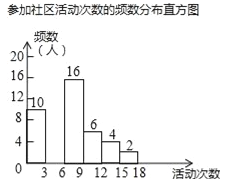
【题目】某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
参加社区活动次数的频数、频率分布表

根据以上图表信息,解答下列问题:
(1)表中a= ,b= ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=4,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

(1)请按照上述思路完成小明遇到的这个问题
(2)参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠DGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年为更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如图的调查问卷(单选).在随机调查了某市全部10000名司机中的部分司机后,统计整理并制作了如下的统计图: 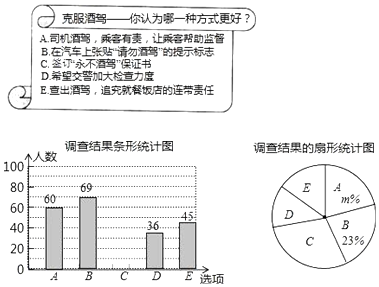
根据以上信息解答下列问题:
(1)补全条形统计图,并计算扇形统计图中m=;
(2)该市支持选项C的司机大约有多少人?
(3)若要从该市支持选项C的司机中随机选择200名,给他们签订“永不酒驾”的保证书,则支持该选项的司机小李被选中的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(5,0)两点,直线y=﹣ ![]() x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式;
(2)若PE=5EF,求m的值;
(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△BOD都是等腰直角三角形,∠ACB=∠BDO=90°,且点A在反比例函数![]() (k>0)的图像上,若OB2-AB2=10,则k的值为 ( )
(k>0)的图像上,若OB2-AB2=10,则k的值为 ( )
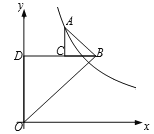
A. 10 B. 5 C. 20 D. 2.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com