
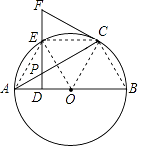
【题目】如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PD⊥AB,垂足为D,射线DP交 ![]() 于点E,交过点C的切线于点F.
于点E,交过点C的切线于点F. 
(1)求证:FC=FP;
(2)若∠CAB=30°,当E是 ![]() 的中点时,判断以A,O,C,E为顶点的四边形是什么特殊四边形,并说明理由.
的中点时,判断以A,O,C,E为顶点的四边形是什么特殊四边形,并说明理由.
【答案】
(1)证明:连接OC
∵CF是⊙O的切线,
∴OC⊥CF,
∴∠FCA+∠ACO=90°,
∵OC=OA,
∴∠OCA=∠OAC,
∵PD⊥AB,
∴∠PAD+∠APD=90°,
而∠APD=∠CPF,
∴∠PAD+∠CPF=90°,
∴∠FCP=∠FPC,
∴FC=FP;
(2)解:以A,O,C,E为顶点的四边形是菱形,
理由如下:
∵∠CAB=30°,
∴∠ABC=60°,从而∠AOC=120°,
∵E是 ![]() 的中点,
的中点,
∴∠AOE=∠EOC=60°,
∴△AOE、△EOC均是等边三角形,
∴AE=AO=OC=CE,
∴四边形AOCE是菱形.
【解析】(1)连接OC,根据切线的性质得出OC⊥CF以及∠OAC=∠OCA得∠FCP=∠FPC,可证得结论;(2)由∠CAB=30°易得△AOE、△EOC均是等边三角形,可得AE=AO=OC=CE,易得以A,O,C,E为顶点的四边形是菱形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、EFGH、NHMC都是正方形,边长分别为a,b,c;A,B,N,E,F五点在同一直线上,则c=(用含有a,b的代数式表示). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移得到△A1B1C1,且点P的对应点为P1(a+5,b+4).
(1)写出△A1B1C1的三个顶点的坐标;
(2)求△ABC的面积;
(3)请在平面直角坐标系中画出△A1B1C1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线PQ∥MN,点A在直线PQ上,点C,D在直线MN上,连接AC,AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE与CE相交于点E.
(1)求∠AEC的度数;
(2)若将图①中的线段AD沿MN向右平移到A1D1如图②所示位置,此时A1E平分∠AA1D1,
CE平分∠ACD1,A1E与CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度数;
(3)若将图①中的线段AD沿MN向左平移到A1D1如图③所示位置,其他条件与(2)相同,求此时∠A1EC的度数(直接写出结果).



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)把数轴补充完整;
(2)在数轴上表示下列各数: 3, ![]() ,
, ![]() ,
, ![]() ;
;
(3)用“<”连接起来.________________________________;
(4)![]() 与
与![]() 之间的距离是_______________.
之间的距离是_______________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是 ( )

A. A1(4,4),C1(3,2) B. A1(3,3),C1(2,1)
C. A1(4,3),C1(2,3) D. A1(3,4),C1(2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,下列说法不正确的是( )

A. 汽车在行驶途中停留了0.5小时
B. 汽车在行驶途中的平均速度为![]() 千米/小时
千米/小时
C. 汽车共行驶了240千米
D. 汽车自出发后3小时至4.5小时之间行驶的速度是80千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,P、Q分别是边AB、BC上的两个动点,P、Q同时分别从A、B出发,点P沿AB向B运动;点Q沿BC向C运动,速度都是1个单位长度/秒.运动时间为t秒. 
(1)连结AQ、DP相交于点F,求证:AQ⊥DP;
(2)当正方形边长为4,而t=3时,求tan∠QDF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com