
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式请你观察下列几种简单多面体模型,解答下列问题:

(1)根据上面多面体的模型,完成表格中的空格:
多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
四面体 | 4 | 4 | |
长方体 | 8 | 12 | |
正八面体 | 8 | 12 | |
正十二面体 | 20 | 12 | 30 |
(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是E=________;
(3)一个多面体的面数比顶点数大8,棱数为30,则这个多面体的面数是多少?
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
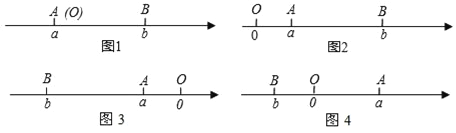
【题目】阅读下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|,当A、B两点都不在原点时.
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示﹣2和5的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2那么x为 .
(3)若x表示一个有理数,则|x﹣1|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件:①.在足球比赛中,中国男足战胜德国男足;②.有交通信号灯的路口遇到红灯;③.连续两次抛掷一枚普通的正方体骰子得到的点数之和为13;④.任取一数为x,使它满足x3=x2.其中随机事件有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l与直线l外一点P,求作:过点P且垂直于直线l的垂线a(尺规作图).
现给出一种作法,如下:
步骤一:在直线l外取一点E,以点P为圆心,以线段PE为半径画弧,交直线l于点M,N;
步骤二:分别以点M、N为圆心,大于![]() 线段MN为半径画弧,过两弧的交点的直线a就是所求作的垂线.
线段MN为半径画弧,过两弧的交点的直线a就是所求作的垂线.
(1)按上述操作步骤,请成功作出过点P且垂直于直线l的垂线a.(符合要求的一种图形),并说明理由.
(2)从你作图的过程中,思考要保证这种作法顺利作出,线段PE应该满足什么条件?
(3)为了避免这种情况产生,小明说只要在直线l上取点E好了,并给出了画法,画法对吗?请说明理由.
(作法:在直线l上取两点B、D,以P为圆心,以PD 为半径画圆交直线l于点E,以P为圆心,以PB 为半径画圆交直线l于点F,其中较小圆分别交PB,PF于点M、N,连接E、N和D、M,EN和MD相交于点H,则PH就是所求的垂线.)
(4)请在直线l上取点E,用直尺和圆规过点P且垂直于直线l的垂线a(与小明不同的方法,并要求尽可能简单).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点.如果两个正方形的边长都等于2,那么正方形A′B′C′OA绕O点无论怎样转动,两个正方形重叠的部分的面积是 . 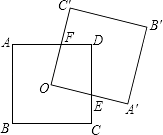
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,与y轴交于点C.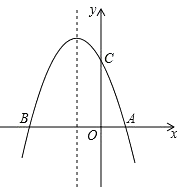
(1)求B、C两点的坐标;
(2)在该抛物线的对称轴上是否存在点P,使得△PAC的周长最小?若存在,求出点P的坐标;若不存在,请说明理由;
(3)抛物线在第二象限内是否存在一点Q,使△QBC的面积最大?,若存在,求出点Q的坐标及△QBC的面积最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com