练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图4­2­22，在△ABC中，AB＝CB，∠ABC＝90°，D为AB延长线上一点，点E在BC边上，且BE＝BD，连接AE，DE，DC.

    (1)求证：△ABE≌△CBD；

    (2)若∠CAE＝30°，求∠BDC的度数．


     (1)证明：∵∠ABC＝90°，∴∠DBE＝180°－∠ABC＝90°.

    ∴∠ABE＝∠CBD.

    在△ABE和△CBD中，

    ∴△ABE≌△CBD(SAS)．

    (2)解：∵AB＝CB，∠ABC＝90°，

    ∴△ABC是等腰直角三角形．∴∠ECA＝45°.

    ∵∠CAE＝30°，∠BEA＝∠ECA＋∠EAC，

    ∴∠BEA＝45°＋30°＝75°.

    由①知∠BDC＝∠BEA，∴∠BDC＝75°.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    若⊙O的半径为4 cm，点A到圆心O的距离为3 cm，那么点A与⊙O的位置关系是(　　)

    A．点A在圆内  B．点A在圆上  C．点A在圆外  D．不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分解因式：x2－y2－3x－3y＝__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    点A是双曲线与直线在第二象限的交点，AB垂直轴于点B，且S△ABO=；（1）求两个函数的表达式

    （2）求直线与双曲线的交点坐标和△AOC的面积。

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


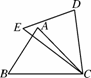
    如图4­2­17，在△ABC和△DEC中，已知AB＝DE，还需要添加两个条件才能使△ABC≌△DEC，不能添加的一组是(　　)

    A．BC＝EC，∠B＝∠E  B．BC＝EC, AC＝DC

    C．BC＝DC，∠A＝∠D  D．∠B＝∠E，∠A＝∠D

        

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    用配方法解一元二次方程x2－2x－3＝0时，方程变形正确的是(　　)

    A．(x－1)2＝2  B．(x－1)2＝4  C．(x－1)2＝1　  D．(x－1)2＝7

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解方程： (x－3)2＋4x(x－3)＝0.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    对于实数x，我们规定[x]表示不大于x的最大整数，例如[1.2]＝1，[3]＝3，[－2.5]＝－3，若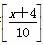＝5，则x的取值可以是(　　)

    A．40　　  B．45　  C．51　  D．56

    查看答案和解析>>

    科目：初中数学 来源： 题型：


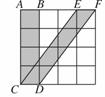
    如图4­3­37,4×4的方格中每个小正方形的边长都是1，则S四边形ABDC与S四边形ECDF的大小关系是(　　)

    A．S四边形ABDC＝S四边形ECDF  B．S四边形ABDC < S四边形ECDF

    C．S四边形ABDC＝S四边形ECDF＋1  D．S四边形ABDC＝S四边形ECDF＋2

    查看答案和解析>>

    同步练习册答案