
| 销售量p(件) | P=45-x |
| 销售单价q(元/件) | 当1≤x≤18时,q=20+x 当18<x≤30时,q=38 |
分析 (1)根据总价=单价×数量,分别用每件商品的利润乘以这种商品的销售量,求出y关于x的函数关系式即可.
(2)首先分类讨论,求出①当1≤x≤18时,②当18<x≤30时,该超市销售这种商品所获的利润是多少,然后比较大小,判断出该超市销售这种商品第几天的利润最大,最大利润是多少即可.
解答 解:(1)①当1≤x≤18时,
y=(20+x-15)(45-x)
=(5+x)(45-x)
=-x2+40x+225
②当18<x≤30时,
y=(38-15)(45-x)
=23(45-x)
=-23x+1035
∴y=$\left\{\begin{array}{l}{-{x}^{2}+40x+225(1≤x≤18)}\\{-23x+1035(18<x≤30)}\end{array}\right.$;
(2)①当1≤x≤18时,y=-(x-20)2+625,
∴当x=18时,y最大值=621元.
②当18<x≤30时,
∵-30<0,
∴y随x的增大而减小,
又∵x取正整数,
∴当x=19时,y最大值=598(元).
∵621>598,
∴在这30天中,该超市销售这种商品,第18天的利润最大,且最大利润为621元.
点评 此题主要考查了二次函数的应用,考查了单价、总价、数量的关系,以及函数解析式的求法,要熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
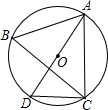 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
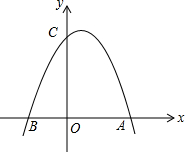 如图,已知抛物线经过点A(3,0)、B(-2,0)、C(0,6).
如图,已知抛物线经过点A(3,0)、B(-2,0)、C(0,6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com