
【题目】手机给学生带来方便的同时也带来了很大的影响.新化县某校初一年级在一次家长会上对若干家长进行了一次对“学生使用手机”现象看法的调查,将调查数据整理得如下统计图(![]() :绝对弊大于利,
:绝对弊大于利,![]() :绝对利大于弊,
:绝对利大于弊,![]() :相对弊大于利,
:相对弊大于利,![]() :相对利大于弊):
:相对利大于弊):
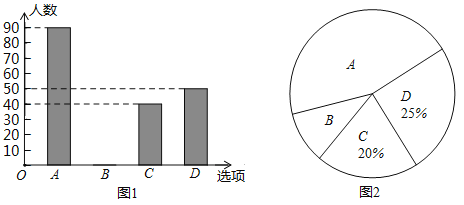
(1)这次调查的家长总人数为多少人?
(2)本次调查的家长中表示“![]() 绝对利大于弊”所占的百分比是多少?并补全条形统计图.
绝对利大于弊”所占的百分比是多少?并补全条形统计图.
(3)求扇形统计图图2中表示“![]() :绝对弊大于利”的扇形的圆心角度数.
:绝对弊大于利”的扇形的圆心角度数.
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为2000m2的区域进行绿化,安排甲、乙两个工程队完成,已知甲队每天完成绿化的面积是乙队每天完成绿化的面积的2倍,并且在独立完成面积为600m2区域的绿化时,甲队比乙队少用6天.
(1)甲、乙两个工程队每天能完成绿化的面积分别是多少?
(2)若学校每天需付给甲队的绿化费用为0.5万元,乙队为0.3万元,要使这次的绿化总费用不超过10万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
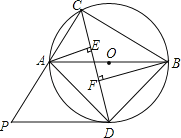
(1)求证:DP∥AB;
(2)若AC=6,BC=8,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,![]() ,求
,求![]() 的度数. (提示:作
的度数. (提示:作![]() ).
).
(2)如图2,![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() ,求
,求![]() 与
与![]() 、
、![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点![]() 在射线
在射线![]() 上运动,请你直接写出
上运动,请你直接写出![]() 与
与![]() 、
、![]() 之间的数量关系.
之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=8,BC=5,以点A为圆心,以任意长为半径作弧,分别交AD、AB于点P、Q,再分别以P、Q为圆心,以大于![]() PQ的长为半径作弧,两弧在∠DAB内交于点M,连接AM并延长交CD于点E,则CE的长为( )
PQ的长为半径作弧,两弧在∠DAB内交于点M,连接AM并延长交CD于点E,则CE的长为( )
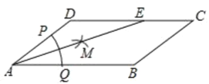
A. 3B. 5C. 2D. 6.5
查看答案和解析>>
科目:初中数学 来源: 题型:
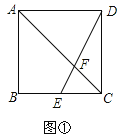
【题目】如图,点E是矩形ABCD的边BC的中点,连接DE交AC于点F.
![]() 如图
如图![]() ,求证:
,求证:![]() ;
;
![]() 如图
如图![]() ,作
,作![]() 于G,试探究:当AB与AD满足什么关系时,使得
于G,试探究:当AB与AD满足什么关系时,使得![]() 成立?并证明你的结论;
成立?并证明你的结论;
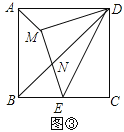
![]() 如图
如图![]() ,以DE为斜边在矩形ABCD内部作等腰
,以DE为斜边在矩形ABCD内部作等腰![]() ,交对角线BD于N,连接AM,若
,交对角线BD于N,连接AM,若![]() ,请直接写出
,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后解答问题(1)、(2)
解方程:|x+3|=2.
当x+30时,原方程可化为:x+3=2,解得x=1;
当x+3<0时,原方程可化为:x+3=2,解得x=5.
所以原方程的解是x=1,x=5.
(1)解方程:|3x1|5=0;
(2)探究:当b为何值时,方程|x2|=b+1①无解;②只有一个解;③有两个解.
查看答案和解析>>
科目:初中数学 来源: 题型:
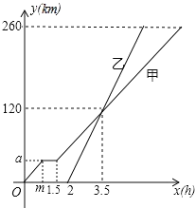
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
(1)直接写出图中m,a的值;
(2)求出甲车行驶路程y(km)与时间x (h)的函数解析式,并写出相应的x的取值范围;
(3)当乙车出发多长时间后,两车恰好相距40km?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com