
 如图,在5×4的方格纸中(每个小正方形的边长均为1)有一条线段AB,其端点均在小正方形的顶点上,请按要求画出图形并计算:
如图,在5×4的方格纸中(每个小正方形的边长均为1)有一条线段AB,其端点均在小正方形的顶点上,请按要求画出图形并计算:分析 (1)把AB=$\sqrt{5}$看作底,高为2$\sqrt{5}$,由此即可解决问题.
(2)如图把AE=3,作为底,高为2,面积正好是3,∠AEB=45°满足条件.
(3)根据勾股定理计算即可求解.
解答 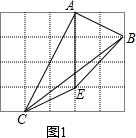 解:(1)如图,△ABC即为所求.
解:(1)如图,△ABC即为所求.
∵∠A=90°,AC=2$\sqrt{5}$,AB=$\sqrt{5}$,
∴S△ABC=$\frac{1}{2}$×2$\sqrt{5}$×$\sqrt{5}$=5.
(2)如图,△ABE即为所求.
S△ABE=$\frac{1}{2}$×3×2=3,∠E=45°.
(3)CE=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
点评 本题考查作图-复杂作图、三角形面积、勾股定理等知识,解题的关键是利用数形结合的思想解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在菱形ABCD中,过点A作AE⊥BC,BC于点E,若菱形ABCD的面积为24,AE=4,则AB的长为( )
如图,在菱形ABCD中,过点A作AE⊥BC,BC于点E,若菱形ABCD的面积为24,AE=4,则AB的长为( )| A. | 12 | B. | 6 | C. | $\sqrt{13}$ | D. | 2$\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.设AP=x.当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式及定义域.
如图,将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.设AP=x.当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式及定义域.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解我省中学生的视力情况 | B. | 了解九(1)班学生校服的尺码情况 | ||
| C. | 检测一批电灯泡的使用寿命 | D. | 调查《体育新闻》栏目的收视率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com