
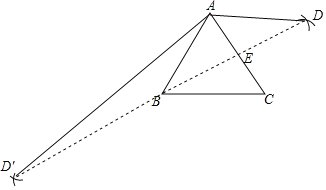
【题目】如图,已知边长为2的等边三角形ABC中,分别以点A,C为圆心,m为半径作弧,两弧交于点D,连结BD.若BD的长为2![]() ,则m的值为_____.
,则m的值为_____.

【答案】2或2![]() .
.
【解析】
由作图知,点D在AC的垂直平分线上,得到点B在AC的垂直平分线上,求得BD垂直平分AC,设垂足为E,得到BE=![]() ,当点D、B在AC的两侧时,如图,证出BE=DE,即可求出m;当点D、B在AC的同侧时,如图,解直角三角形即可得到结论.
,当点D、B在AC的两侧时,如图,证出BE=DE,即可求出m;当点D、B在AC的同侧时,如图,解直角三角形即可得到结论.
解:由作图知,点D在AC的垂直平分线上,
∵△ABC是等边三角形,
∴点B在AC的垂直平分线上,
∴BD垂直平分AC,
设垂足为E,
∵AC=AB=2,
∴BE=AB·sin60°=![]() ,
,
当点D、B在AC的两侧时,如图,
∵BD=2![]() ,
,
∴BE=DE,
∴AD=AB=2,
∴m=2;
当点D、B在AC的同侧时,如图,
∵![]() =2
=2![]() ,
,
∴![]() =3
=3![]() ,
,
∴![]() =
=![]() =2
=2![]() ,
,
∴m=2![]() ,
,
综上所述,m的值为2或2![]() ,
,
故答案为:2或2![]() .
.


科目:初中数学 来源: 题型:
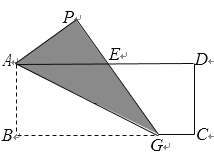
【题目】如图,矩形纸片ABCD中,AB=4,BC=10,G是BC边上一点,沿AG折叠△ABG,点B的落点为P,GP交AD于点E. 若E是AD的中点,则BG的长是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小雨、小华、小星暑假到某超市参加社会实践活动,在活动中他们参加了某种水果的销售工作,已知该水果的进价为8元![]() 千克.他们通过市场调查发现:当销售单价为10元/千克时,那么每天可售出300千克;销售单价每上涨1元,每天的销售量就减少50千克.
千克.他们通过市场调查发现:当销售单价为10元/千克时,那么每天可售出300千克;销售单价每上涨1元,每天的销售量就减少50千克.
(1)该超市销售这种水果,当销售单价不低于10元/千克时,请直接写出每天的销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元
(元![]() 千克)之间的函数关系式;
千克)之间的函数关系式;
(2)一段时间后,发现这种水果每天的销售量均不低于250千克,则此时该超市销售这种水果每天获取的利润![]() (元
(元![]() 最大是多少?
最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:连结凸四边形一组对边中点的线段叫做四边形的“准中位线”.
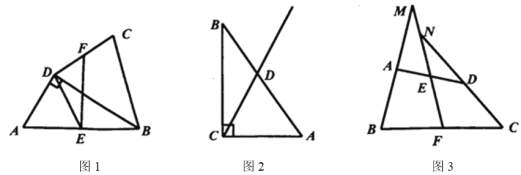
(1)概念理解:
如图1,四边形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 是
是![]() 边上一点,满足
边上一点,满足![]() ,试判断
,试判断![]() 是否为四边形
是否为四边形![]() 的准中位线,并说明理由.
的准中位线,并说明理由.
(2)问题探究:
如图2,![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 以每秒1个单位的速度,从点
以每秒1个单位的速度,从点![]() 出发向点
出发向点![]() 运动,动点
运动,动点![]() 以每秒6个单位的速度,从点
以每秒6个单位的速度,从点![]() 出发沿射线
出发沿射线![]() 运动,当点
运动,当点![]() 运动至点
运动至点![]() 时,两点同时停止运动.
时,两点同时停止运动.![]() 为线段
为线段![]() 上任意一点,连接并延长
上任意一点,连接并延长![]() ,射线
,射线![]() 与点
与点![]() 构成的四边形的两边分别相交于点
构成的四边形的两边分别相交于点![]() ,设运动时间为
,设运动时间为![]() .问
.问![]() 为何值时,
为何值时,![]() 为点
为点![]() 构成的四边形的准中位线.
构成的四边形的准中位线.
(3)应用拓展:
如图3,![]() 为四边形
为四边形![]() 的准中位线,
的准中位线,![]() ,延长
,延长![]() 分别与
分别与![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,请找出图中与
,请找出图中与![]() 相等的角并证明.
相等的角并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像分别交于点
的图像分别交于点![]() 和点B.
和点B.
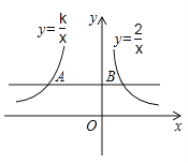
![]() 若
若![]() 线段
线段![]() 的长度是
的长度是![]() ,求点
,求点![]() 的坐标及
的坐标及![]() 的值;
的值;
![]() 嘉淇同学观察了三个函数图像后,大胆猜想:“当
嘉淇同学观察了三个函数图像后,大胆猜想:“当![]() 一定时,
一定时,![]() 的面积一定随
的面积一定随![]() 的增大而增大.”你认为他的猜想对吗.说明理由;
的增大而增大.”你认为他的猜想对吗.说明理由;
![]() 在
在![]() 的条件下,若直线
的条件下,若直线![]() 与
与![]() 的图像有交点,与
的图像有交点,与![]() 的图像无交点,请直接写出
的图像无交点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1为搭建在地面上的遮阳棚,图2、图3是遮阳棚支架的示意图.遮阳棚支架由相同的菱形和相同的等腰三角形构成,滑块E,H可分别沿等长的立柱AB,DC上下移动,AF=EF=FG=1m.
(1)若移动滑块使AE=EF,求∠AFE的度数和棚宽BC的长.
(2)当∠AFE由60°变为74°时,问棚宽BC是增加还是减少?增加或减少了多少?(结果精确到0.1m.参考数据:![]() ≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们寒假期间每天健身的时间![]() (分),校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表,已知
(分),校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表,已知![]() 组所在扇形的圆心角为
组所在扇形的圆心角为![]() .
.
组别 | 频数统计 |
| 8 |
| 12 |
|
|
| 15 |
| b |
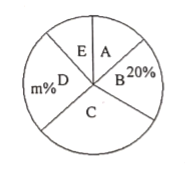
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有 人,![]() ,
,![]() ,
,![]() ;
;
(2)求扇形统计图中扇形![]() 的圆心角度数;
的圆心角度数;
(3)该校共有学生1200人,请估计每天健身时间不少于1小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,图2,△ABC是等边三角形,D、E分别是AB、BC边上的两个动点(与点A、B、C不重合),始终保持BD=CE.
(1)当点D、E运动到如图1所示的位置时,求证:CD=AE.
(2)把图1中的△ACE绕着A点顺时针旋转60°到△ABF的位置(如图2),分别连结DF、EF.
①找出图中所有的等边三角形(△ABC除外),并对其中一个给予证明;
②试判断四边形CDFE的形状,并说明理由.
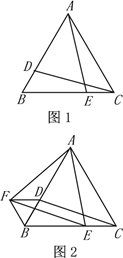
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰△ABC的顶角∠A=36°(如图).
(1)请用尺规作图法作底角∠ABC的平分线BD,交AC于点D(保留作图痕迹,不要求写作法);
(2)证明:△ABC∽△BDC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com