
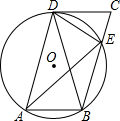
 如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.
如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.分析 (1)根据圆内接四边形的性质得∠BAD+∠BED=180°,则利用等角的补角相等得到∠DEC=∠BAD,再根据平行四边形的性质得∠C=∠BAD,AB=CD=3,则∠C=∠DEC,于是得到DE=DC=3;
(2)作直径DF,连结AF,如图,由圆周角定理得∠DAF=90°,∠EDF=∠EAF,加上∠CDE=∠DAE,则∠CDE+∠EDF=∠DAE+∠EAF,即∠CDF=90°,所以OF⊥CD,然后根据切线的判定定理可判断直线DC与⊙O相切.
解答 解:(1)∵四边形ABED为圆内接四边形,
∴∠BAD+∠BED=180°,
而∠BED+∠DEC=180°,
∴∠DEC=∠BAD,
∵四边形ABCD为平行四边形,
∴∠C=∠BAD,AB=CD=3,
∴∠C=∠DEC,
∴DE=DC=3;
(2)直线DC与⊙O相切.理由如下:
作直径DF,连结AF,如图,
∵DF为直径,
∴∠DAF=90°,
∵∠EDF=∠EAF,
而∠CDE=∠DAE,
∴∠CDE+∠EDF=∠DAE+∠EAF,即∠CDF=90°,
∴OF⊥CD,
∴直线DC与⊙O相切.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了平行四边形的性质.


科目:初中数学 来源: 题型:选择题
 甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前
甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前| A. | 乙比甲晚出发1小时 | B. | 甲比乙晚到B地3小时 | ||
| C. | 甲的速度是4千米/小时 | D. | 乙的速度是10千米/小时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某空军加油飞机给另一架正在飞行的运输飞机进行空中加油,在加油的过程中,设运输飞机的油箱余油量为y1(吨).加油飞机的油箱余油量为y2(吨),已知y1(吨),y2(吨)与加油时间t(分)之间的函数关系图象如图所示.
某空军加油飞机给另一架正在飞行的运输飞机进行空中加油,在加油的过程中,设运输飞机的油箱余油量为y1(吨).加油飞机的油箱余油量为y2(吨),已知y1(吨),y2(吨)与加油时间t(分)之间的函数关系图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD是△ABC的高,四边形PQRS是矩形,且点P、Q在BC边上,点R在AC边上,点S在AB边上,矩形的长是宽的2倍,其中BC=30cm,AD=20cm.
如图,AD是△ABC的高,四边形PQRS是矩形,且点P、Q在BC边上,点R在AC边上,点S在AB边上,矩形的长是宽的2倍,其中BC=30cm,AD=20cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,点E,F在直线AB上,且AE=AB=BF,连结CE,DF分别交AD,BC于点M,N.
如图,在?ABCD中,点E,F在直线AB上,且AE=AB=BF,连结CE,DF分别交AD,BC于点M,N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com