
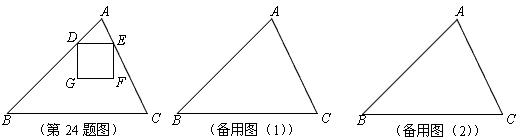
| 解:(1)当正方形DEFG的边GF在BC上时,如图(1),过点A作BC边上的高AM,交DE于N,垂足为M ∵S△ABC=48,BC=12, ∴AM=8 ∵DE∥BC,△ADE∽△ABC ∴  而AN=AM-MN=AM-DE ∴  解之得  ∴当正方形DEFG的边GF在BC上时,正方形DEFG的边长为4.8。 |
 |
| (2)分两种情况: ①当正方形DEFG在△ABC的内部时,如图(2), △ABC 与正方形DEFG重叠部分的面积为正方形DEFG的面积, ∵DE=x, ∴  ,此时x的范围是0<x≤4.8。 ,此时x的范围是0<x≤4.8。 |
 |
| ②当正方形DEFG的一部分在△ABC的外部时,如图(3), 设DG与BC交于点Q,EF与BC交于点P, △ABC的高AM交DE于N, ∵DE=x,DE∥BC, ∴△ADE∽△ABC 即  而AN=AM-MN=AM-EP ∴  解得  所以  即  由题意,x>4.8,x<12, 所以  因此△ABC与正方形DEFG重叠部分的面积为  当0<x≤4.8时,△ABC与正方形DEFG重叠部分的面积的最大值为4.82=23.04 当  时,因为 时,因为 所以当  时 时△ABC与正方形DEFG重叠部分的面积的最大值为  因为24>23.04, 所以△ABC与正方形DEFG重叠部分的面积的最大值为24。 |
 |


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
 (1)如图,在锐角三角形ABC中,BC=12,sinA=
(1)如图,在锐角三角形ABC中,BC=12,sinA=| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在锐角三角形ABC中,AD⊥BC,AD=12cm,AB=13cm,BC=14cm,则AC的长为( )
如图,在锐角三角形ABC中,AD⊥BC,AD=12cm,AB=13cm,BC=14cm,则AC的长为( )| A、12cm | B、13cm | C、14cm | D、15cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com