Question

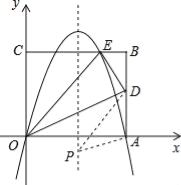
【题目】如图，矩形的边OA在x轴上，边OC在y轴上，点B的坐标为（10，8），沿直线OD折叠矩形，使点A正好落在BC上的E处，E点坐标为（6，8），抛物线y=ax2+bx+c经过O、A、E三点．

（1）求此抛物线的解析式；

（2）求AD的长；

（3）点P是抛物线对称轴上的一动点，当△PAD的周长最小时，求点P的坐标．

Answer 1

【答案】（1）y=；（2）AD=5；（3）（5，）

【解析】

试题分析：（1）利用矩形的性质和B点的坐标可求出A点的坐标，再利用待定系数法可求得抛物线的解析式；（2）设AD=x，利用折叠的性质可知DE=AD，在Rt△BDE中，利用勾股定理可得到关于x的方程，可求得AD的长；（3）由于O、A两点关于对称轴对称，所以连接OD，与对称轴的交点即为满足条件的点P，利用待定系数法可求得直线OD的解析式，再由抛物线解析式可求得对称轴方程，从而可求得P点坐标．

试题解析：（1）∵四边形ABCD是矩形，B（10，8），

∴A（10，0）， 又抛物线经过A、E、O三点，把点的坐标代入抛物线解析式可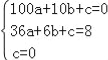得，解得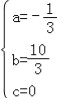， ∴抛物线的解析式为y=﹣x2+x；

（2）由题意可知：AD=DE，BE=10﹣6=4，AB=8， 设AD=x，则ED=x，BD=AB﹣AD=8﹣x，

在Rt△BDE中，由勾股定理可知ED2=EB2+BD2，即x2=42+（8﹣x）2，解得x=5， ∴AD=5；

（3）∵y=﹣x2+x， ∴其对称轴为x=5， ∵A、O两点关于对称轴对称， ∴PA=PO，

当P、O、D三点在一条直线上时，PA+PD=PO+PD=OD，此时△PAD的周长最小，

如图，连接OD交对称轴于点P，则该点即为满足条件的点P，

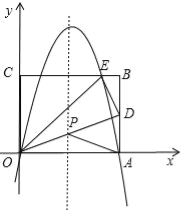
由（2）可知D点的坐标为（10，5），

设直线OD解析式为y=kx，把D点坐标代入可得5=10k，解得k=， ∴直线OD解析式为y=x，

令x=5，可得y=， ∴P点坐标为（5，）．