
分析 当3是腰时,把x=3代入方程就可以求出m的值,再将m的值代入解得x,求得另一边,可得结果;当3是底时,则AB=AC,原方程有两个相等的实数根根据△=0就可以求出m的值,同理可得结果.
解答 解:当3是等腰三角形的腰时,9-(m+2)×3+2m=0,
解得:m=3.
∴x2-(m+2)x+2m=0为x2-5x+6=0
解得x1=2,x2=3,
∴等腰三角形的三边为3,3,2,
符合构成三角形的条件,
∴等腰△ABC的周长是3+3+2=8;
当3是等腰三角形的底时,
∴AB=AC,
∴方程x2-(m+2)x+2m=0有两个相等的实根,
∴△=0,
∴[-(m+2)]2-4×2m=0,
m=2,
∴x2-(m+2)x+2m=0为x2-5x+6=0
解得:x1=x2=2,
∴等腰三角形的三边为3,2,2,
符合构成三角形的条件,
∴等腰△ABC的周长是3+2+2=7;
综上所述∴等腰△ABC的周长是7或8.
故答案为:7或8.
点评 本题考查了等腰三角形的性质的运用,根与系数的关系的运用,一元一次方程的解法的运用,解答时分类讨论是关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题
| 技术 | 上场时间 | 投篮次数 | 投中次数 | 罚球得分 | 篮板个数 | 助攻次数 | 个人总得分 |
| 数据 | 45 | 27 | 14 | 7 | 13 | 12 | 41 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
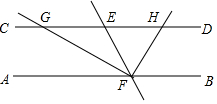 如图,直线EF分别与直线AB,CD相交于点F,E,FG平分∠AFE交CD于点G,FH平分∠BFE交CD于点H,若∠GEF=7∠FGE,AB∥CD,那么∠HFB=70°.
如图,直线EF分别与直线AB,CD相交于点F,E,FG平分∠AFE交CD于点G,FH平分∠BFE交CD于点H,若∠GEF=7∠FGE,AB∥CD,那么∠HFB=70°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
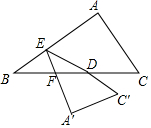 在Rt△ABC中,AC=3,AB=4,D为斜边BC中点,E为AB上一个动点,将△ABC沿直线DE折叠,A、C的对应点分别为A′、C′,EA′交BC于点F,若△BEF为直角三角形,则BE的长度为$\frac{1}{2}$或$\frac{5}{4}$.
在Rt△ABC中,AC=3,AB=4,D为斜边BC中点,E为AB上一个动点,将△ABC沿直线DE折叠,A、C的对应点分别为A′、C′,EA′交BC于点F,若△BEF为直角三角形,则BE的长度为$\frac{1}{2}$或$\frac{5}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为10$\sqrt{5}$.
如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为10$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com