
【题目】在矩形ABCD中,AB=6,AD=2 ![]() ,E是AB边上一点,AE=2,F是直线CD上一动点,将△AEF沿直线EF折叠,点A的对应点为点A′,当点E、A′、C三点在一条直线上时,DF的长度为 .
,E是AB边上一点,AE=2,F是直线CD上一动点,将△AEF沿直线EF折叠,点A的对应点为点A′,当点E、A′、C三点在一条直线上时,DF的长度为 . 
【答案】6+2 ![]() 或6﹣2
或6﹣2 ![]()
【解析】解:如图1,
F是线段CD上一动点,由翻折可知,∠FEA=∠FEA′,
∵CD∥AB,
∴∠CFE=∠AEF,
∴∠CFE=∠CEF,
∴CE=CF,
在Rt△BCE中,EC= ![]() =
= ![]() =2
=2 ![]() ,
,
∴CF=CE=2 ![]() ,
,
∵AB=CD=6,
∴DF=CD﹣CF=6﹣2 ![]() ,
,
如图2,
F是DC延长线上一点,由翻折可知,∠FEA=∠FEA′,
∵CD∥AB,
∴∠CFE=∠AEF,
∴∠CFE=∠CEF,
∴CE=CF,
在Rt△BCE中,EC= ![]() =
= ![]() =2
=2 ![]() ,
,
∴CF=CE=2 ![]() ,
,
∵AB=CD=6,
∴DF=CD+CF=6+2 ![]() ,
,
所以答案是6+2 ![]() 或6﹣2
或6﹣2 ![]() .
.
【考点精析】掌握矩形的性质和翻折变换(折叠问题)是解答本题的根本,需要知道矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,其对称轴为直线x=1,给出下列结论:
①b2-4ac>0;②2a+b=0;③abc>0;④3a+c>0.
则正确的结论个数为( )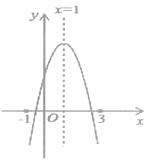
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 ![]() 的图象如图.
的图象如图.
(1)求它的对称轴与x轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,D是斜边AB的中点,AC=4,BC=2,将△ACD沿直线CD折叠,点A落在点E处,联结AE,那么线段AE的长度等于 . 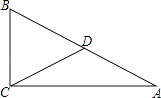
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y= ![]() (k>0)的图象与BC边交于点E.
(k>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AD与塔CB之间的距离AC长为27m,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,分别求大楼AD的高与塔BC的高(结果精确到0.1m,参考数据: ![]() ≈2.24,
≈2.24, ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)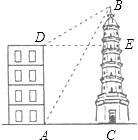
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一公路的道路维修工程,准备从甲、乙两个工程队选一个队单独完成.根据两队每天的工程费用和每天完成的工程量可知,若由两队合做此项维修工程,6天可以完成,共需工程费用385200元,若单独完成此项维修工程,甲队比乙队少用5天,每天的工程费用甲队比乙队多4000元,从节省资金的角度考虑,应该选择哪个工程队?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3 ![]() ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( ) 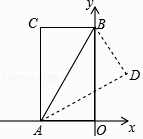
A.( ![]() ,
, ![]() )
)
B.(2, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,3﹣
,3﹣ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com