
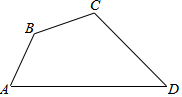
 四边形ABCD中,AB=$\sqrt{6}$,BC=5-$\sqrt{3}$,CD=6,∠ABC=135°,∠BCD=120°,求AD的长.
四边形ABCD中,AB=$\sqrt{6}$,BC=5-$\sqrt{3}$,CD=6,∠ABC=135°,∠BCD=120°,求AD的长. 分析 作AE⊥BC,DE⊥BC,AG⊥DF,则四边形AEFG为矩形,AE=FG.EF=AG,因为△ADG为直角三角形,所以AD=$\sqrt{A{G}^{2}+D{G}^{2}}$,根据直角△AEB和直角△CDF即可求AE,BE,CF,FD.
解答 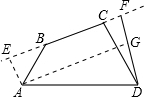 解:作AE⊥BC于E,DF⊥BC于F,AG⊥DF于G,如图所示:
解:作AE⊥BC于E,DF⊥BC于F,AG⊥DF于G,如图所示:
则四边形AEFG四个内角均为直角,
∴四边形AEFG为矩形,AE=FG.EF=AG
∠ABE=180°-135°=45°,∠DCF=180°-120°=60°,
∴AE=EB=$\sqrt{6}$×$\frac{\sqrt{2}}{2}$=$\sqrt{3}$,CF=$\frac{1}{2}$×CD=3,FD=$\sqrt{3}$CF=3 $\sqrt{3}$,
∴AG=EF=8,DG=DF-AE=2 $\sqrt{3}$,
∴AD=$\sqrt{A{G}^{2}+D{G}^{2}}$=2 $\sqrt{19}$.
点评 本题考查了矩形的判定和矩形对边相等的性质,考查了勾股定理在直角三角形中的运用,本题中构造矩形AEFG是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 定义运算“※”为:a※b=$\left\{\begin{array}{l}{ab(b≥0)}\\{-ab(b<0)}\end{array}\right.$
定义运算“※”为:a※b=$\left\{\begin{array}{l}{ab(b≥0)}\\{-ab(b<0)}\end{array}\right.$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知A(-3,n),B(2,-3)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-3,n),B(2,-3)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com