
分析 (1)先根据题意得出$\frac{1}{x}$与$\frac{1}{y}$的值,再代入代数式进行计算即可;
(2)先把代数式的分子分母同时除以x2y2,再把出$\frac{1}{x}$与$\frac{1}{y}$的值代入进行计算即可.
解答 解:(1)∵x=$\frac{1}{\sqrt{2}-\sqrt{3}+1}$,y=$\frac{1}{\sqrt{2}+\sqrt{3}+1}$,
∴$\frac{1}{x}$=$\sqrt{2}$-$\sqrt{3}$+1,$\frac{1}{y}$=$\sqrt{2}$+$\sqrt{3}$+1,
∴原式=($\sqrt{2}$-$\sqrt{3}$+1)($\sqrt{2}$+$\sqrt{3}$+1)=($\sqrt{2}$+1)2-3=2$\sqrt{2}$;
(2)代数式的分子分母同时除以x2y2得,$\frac{1}{{y}^{2}}$+$\frac{2}{xy}$+$\frac{1}{{x}^{2}}$,
∵$\frac{1}{x}$=$\sqrt{2}$-$\sqrt{3}$+1,$\frac{1}{y}$=$\sqrt{2}$+$\sqrt{3}$+1,
∴原式=($\sqrt{2}$+$\sqrt{3}$+1)2+2($\sqrt{2}$-$\sqrt{3}$+1)($\sqrt{2}$+$\sqrt{3}$+1)+($\sqrt{2}$-$\sqrt{3}$+1)2
=[($\sqrt{2}$+$\sqrt{3}$+1)+($\sqrt{2}$-$\sqrt{3}$+1)]2
=($\sqrt{2}$+$\sqrt{3}$+1+$\sqrt{2}$-$\sqrt{3}$+1)2
=(2$\sqrt{2}$+2)2
=12+8$\sqrt{2}$.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.


科目:初中数学 来源: 题型:选择题
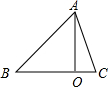 如图,在△ABC中,AO⊥BC,垂足为O,若AO=4,∠B=45°,△ABC的面积为10,则AC边长的平方的值是( )
如图,在△ABC中,AO⊥BC,垂足为O,若AO=4,∠B=45°,△ABC的面积为10,则AC边长的平方的值是( )| A. | 16 | B. | 17 | C. | 6 | D. | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com