
【题目】如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.
(1)求证:AF=CE;
(2)如果AC=EF,且∠ACB=135°,试判断四边形AFCE是什么样的四边形,并证明你的结论
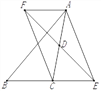
【答案】(1)证明见解析;(2)见解析
【解析】试题分析:根据AF∥CE得到∠AFD=∠CED,∠FAD=∠ECD,根据中点得到AD=CD,则得到△ADF≌△CDE,得出答案;根据全等得到FD=ED,结合D=CD,AC=EF得到四边形为矩形,根据∠AEC=90°,∠ACB=135°,得到∠ACE=∠CAE=45°,则AE=CE,从而说明正方形.
试题解析:(1)证明:∵AF∥CE,
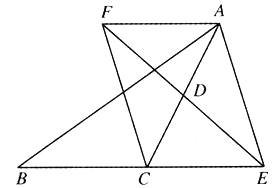
∴∠AFD=∠CED,∠FAD=∠ECD. ∵D是AC的中点,∴AD=CD. ∴△ADF≌△CDE.∴AF=CE.
(2)四边形AECF是正方形.
证明:∵△ADF≌△ CDE,∴FD=ED. 又∵AD=CD,AC=EF, ∴四边形AECF是矩形,
∵∠AEC=90° ∵∠ACB=135°,∠ACE=∠CAE=45° ∴AE=CE.∴四边形AECF是正方形.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F.
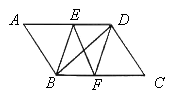
【1】△ABE≌△CDF
【2】若BD⊥EF,则判断四边形EBFD是什么特殊四边形,请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
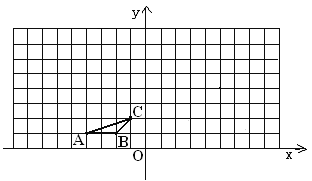
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-2,1)。
(1)画出△ABC绕C点顺时针旋转90°后得到的△A1B1C1并写出A1点的坐标。
(2)以原点O为位似中心,位似比为2,在第二象限内作△ABC的位似图形△A2B2C2,并写出C2的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
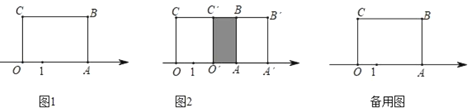
【题目】如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)数轴上点A表示的数为 .
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为OABC,移动后的长方形OABC与原长方形OABC重叠部分(如图8中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A表示的数是 .
②设点A的移动距离AA'=x
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA的中点,点E在找段OO'上,且OO'=3OE,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中的一个正方形剪开得到图③,图③中共有7个正方形;将图③中的一个正方形剪开得到图④,图④中共有10个正方形……如此下去,则第2019个图中共有正方形的个数为( ).
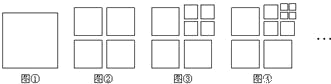
A.6052B.6055C.6058D.6061
查看答案和解析>>
科目:初中数学 来源: 题型:
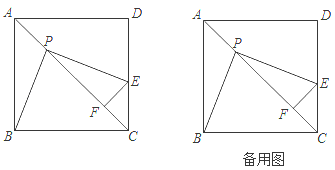
【题目】已知边长为1的正方形ABCD中,P是对角线AC上的一个动点(与点A. C不重合),过点P作PE⊥PB,PE交射线DC于点E,过点E作EF⊥AC,垂足为点F,当点E落在线段CD上时(如图),
(1)求证:PB=PE;
(2)在点P的运动过程中,PF的长度是否发生变化?若不变,试求出这个不变的值,若变化,试说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OB是∠AOC的平分线,OD是∠COE的平分线.
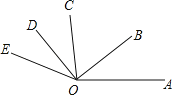
(1)若∠AOB=40°,∠DOE=30°,求∠BOD的度数;
(2)若∠AOD与∠BOD互补,且∠DOE=35°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:射线OP∥AE
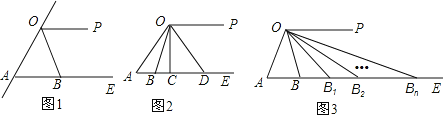
(1)如图1,∠AOP的角平分线交射线AE与点B,若∠BOP=58°,求∠A的度数.
(2)如图2,若点C在射线AE上,OB平分∠AOC交AE于点B,OD平分∠COP交AE于点D,∠ADO=39°,求∠ABO﹣∠AOB的度数.
(3)如图3,若∠A=m,依次作出∠AOP的角平分线OB,∠BOP的角平分线OB1,∠B1OP的角平分线OB2,∠Bn﹣1OP的角平分线OBn,其中点B,B1,B2,…,Bn﹣1,Bn都在射线AE上,试求∠ABnO的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com