
����Ŀ����ѧ���ϣ�����ʦ������������
��ͼ1��ֱ��MN��һ��A������A��ֱ��MN��ƽ���ߣ�

(1)С·���������£�
�� ��MN����ȡһ��B��������BA��
�� ��BΪԲ�����ⳤΪ�뾶�������ֱ�BA��MN��C��D���㣨��Dλ��BA����ࣩ������AΪԲ�ģ���ͬ�ij���Ϊ�뾶����EH����BA�ڵ�E����Eλ�ڵ�A�Ϸ�����
����EΪԲ��CD�ij�Ϊ�뾶����������EH�ڵ�F��F��λ��BA��ࣩ
����ֱ��AF
��ֱ��AF��Ϊ������ƽ���ߣ�
�������С·ͬѧ����ͼ����������ֱ�ߺ�Բ�������ͼ��������ͼ�ۼ��������������������ע�������̺�����ѧ���ݣ�

(2)����ο�С·������������ͼ2�����һ��������A��MN��ƽ�������ij߹���ͼ���̣�������ͼ�ۼ�������˵�������̺�����ѧ���ݣ�
���𰸡���1������������2��������.
��������
��1��������ͼ���̣�����SSS��֤��![]() ���Ӷ��õ�ͬλ����ȣ���ֱ��ƽ�У�
���Ӷ��õ�ͬλ����ȣ���ֱ��ƽ�У�
��2������С·�����������ݡ��ڴ�����ȣ���ֱ��ƽ�С�������ƽ���ߣ�ͬ��������SSS��֤��![]() ���Ӷ��õ��ڴ�����ȣ���ֱ��ƽ�еĽ���.
���Ӷ��õ��ڴ�����ȣ���ֱ��ƽ�еĽ���.
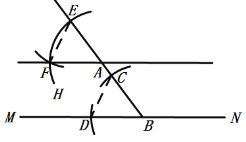
��1��֤������ͼ��������ͼ���̣�֪��![]() ��
��
����EF��AD��
��![]() ��
��![]() ��
��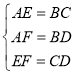 ��
��
��![]() (SSS)��
(SSS)��
��![]() (ͬλ����ȣ���ֱ��ƽ��)
(ͬλ����ȣ���ֱ��ƽ��)
�ʴ�Ϊ��![]() �� ͬλ����ȣ���ֱ��ƽ��
�� ͬλ����ȣ���ֱ��ƽ��
��2����ͼ������
�� ��MN����ȡһ��B��������BA(![]() Ϊ���)��
���)��
�� ��BΪԲ�����ⳤΪ�뾶�������ֱ�BA��BN��C��D���㣨��Dλ��BA���Ҳࣩ������AΪԲ�ģ���ͬ�ij���Ϊ�뾶����EH����BA�ڵ�E����Eλ�ڵ�A�·�����
����EΪԲ��CD�ij�Ϊ�뾶����������EH�ڵ�F��F��λ��BA��ࣩ
����ֱ��AF
��ֱ��AF��Ϊ������ƽ���ߣ�
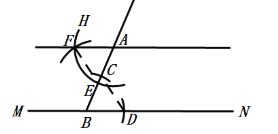
֤������ͼ��������ͼ���̣�֪��![]() ��
��
����EF��AD��
��![]() ��
��![]() ��
��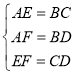 ��
��
��![]() (SSS)��
(SSS)��
��![]() (�ڴ�����ȣ���ֱ��ƽ��)
(�ڴ�����ȣ���ֱ��ƽ��)


 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������˵�������ĸ��Ƕ���ȵ��ı����Ǿ��Σ�����һ��Ա�ƽ�У���������Ϊֱ�ǵ��ı����Ǿ��Σ�������Ա߷ֱ��������һ����Ϊֱ�ǵ��ı����Ǿ��Σ����Խ����������һ������ֱ�ǵ��ı����Ǿ��Σ����Խ�����ƽ������ȵ��ı����Ǿ��Σ����У���ȷ�ĸ����ǣ� ��
A. ![]() �� B.
�� B. ![]() �� C.
�� C. ![]() �� D.
�� D. ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
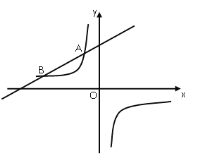
����Ŀ����ͼ��һ�κ���![]() ��
��![]() ��������
Ϊ��������![]() ����ͼ���뷴��������
����ͼ���뷴��������![]() ��ͼ����
��ͼ����![]() ��
��![]() ����.
����.
��1����һ�κ����ı���ʽ��
��2������ֱ��![]() ����ƽ��
����ƽ��![]() ����λ���Ⱥ��뷴����������ͼ������ֻ��һ�������㣬��
����λ���Ⱥ��뷴����������ͼ������ֻ��һ�������㣬��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͨ���ԡ����ɶ�������ѧϰ������֪�������һ���������У����ߵ�ƽ���͵��ڵ����ߵ�ƽ������ô���������һ����ֱ��������.��������¶���һ���������������ߵ�ƽ���͵��ڵ�����ƽ����2���������ν�������������.
��1���������������εĶ��壬�����жϣ��ȱ�������һ����������������
�������������ǣ���
��2����ij�����ε����߳��ֱ�Ϊ1��![]() ��2������������Dz������������Σ��������жϲ�д���ж����ݣ�
��2������������Dz������������Σ��������жϲ�д���ж����ݣ�
��3����![]() �У����߳��ֱ�Ϊ
�У����߳��ֱ�Ϊ![]() ������
������![]() ��������������Dz������������Σ��������жϲ�д���ж����ݣ�
��������������Dz������������Σ��������жϲ�д���ж����ݣ�
̽��:Rt![]() ��,
��,![]() ,��b>a,��Rt
,��b>a,��Rt![]() ��������������
��������������![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A�ڷ���������y=��![]() ��ͼ���ϣ���D�ڷ���������y=
��ͼ���ϣ���D�ڷ���������y=![]() ��k��0����ͼ���ϣ�AD��x�ᣬAB��x����B��DC��x����C����OB=
��k��0����ͼ���ϣ�AD��x�ᣬAB��x����B��DC��x����C����OB=![]() OC����k��ֵΪ_____��
OC����k��ֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)�ⷽ�̣� ![]() ��2��
��2��![]() ��
��
(2)��y��kx����k��0��������ʽ(x��3y)(2x��y)��y(x��5y)����Ľ��Ϊ2x2����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC����AB��AC��D��A��E���㶼��ֱ��m������BDA����AEC����BAC��BD��3��CE��6����DE�ij�Ϊ______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���k2x2��2��k+1��x+1=0������ʵ������
��1����k��ȡֵ��Χ��
��2����k=1ʱ�����������̵��������ֱ�Ϊx1��x2����x1��2����x2��2����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���B����Ϊ(-3��0)����A��y����������һ�㣬��AB=5����P��x����λ�ڵ�B�Ҳ��һ�����㣬���P������Ϊ��m��0��

��1����A������Ϊ( )
��2������ABP�ǵ���������ʱ����P������ꣻ
��3����ͼ2������P��PE��AB���߶�AB�ڵ�E������OE������A����ֱ��OE�ĶԳƵ�ΪA'������A'ǡ������ֱ��PE��ʱ��BE=________(ֱ��д����)
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com